卡方检验是以χ2分布为基础的一种常用假设检验方法，统计样本的实际观测值与理论推断值之间的偏离程度，主要在分类数据资料统计推断中应用。

在电商平台中，广告图到处可见，引起用户兴趣，为商品或者店铺带去流量。表征广告图是否“优秀”的关键数据就是CTR（Click-Through-Rate，点击通过率）。为了设计高CTR图片，电商运营、设计同学们都总结出了一些经验，但这些经验未形成更精细化的设计原则来回答“特定品类下，什么样的广告图CTR最高”。

借助于京东平台沉淀的大量广告图数据，我们希望通过分析历史广告图的数据表现，得到不同品类下高CTR广告图的设计特征，也为后期验证提供初步的数据假设。

我们对广告图包含的设计元素进行了分类打标，但在缺少广告图的CTR具体数据，仅有高低CTR分组数据时，应该如何分析呢？

答案是：卡方检验。

为什么用卡方检验？

定义是什么？

卡方检验是以χ2分布为基础的一种常用假设检验方法，统计样本的实际观测值与理论推断值之间的偏离程度，主要在分类数据资料统计推断中应用，如两个或多个率/构成比之间的比较以及分类资料的相关分析等。

基于这个定义，我们了解到卡方检验的适用范围是“分类数据”，即说明事物类别名称的数据，比如“性别”是一个分类变量，其变量值是“男”或“女”，两者之间无法进行运算或比较。

此案例为什么合适？

此案例中，广告图中不同的设计元素，如装饰元素、设计手法、背景色调等均是分类变量。同时，图片被分为高低CTR两组，也属于分类变量。既然是对两个分类变量（设计因素、高低CTR）做相关分析，卡方检验很适用于此案例。

卡方检验怎么做？

思路是什么？

在基本的假设检验思路上，卡方检验与t检验、F检验等有着相似的过程：

1. 建立无效假设H₀：观察频数与期望频数没有差别（即某一因素设计水平下高低点击率广告图频数与平均频数没有区别）；
2. 在假设H₀成立基础上，计算出χ2值来表征观察值与理论值之间的偏离程度；
3. 根据p值（多设定为0.05）及自由度，根据χ2分布查出拒绝H₀假设的临界值；
4. 若计算得χ2>临界值，即H₀成立的概率＜5%，表示在95%置信水平下，观察值与理论值之间有显著差异；反之，则说明两者无差异。

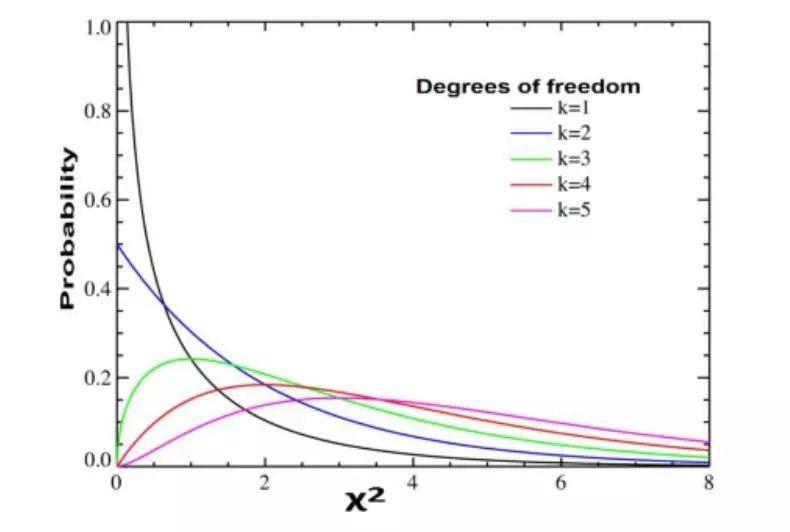
根据这个基本思想及过程，可以看出，χ2、自由度（df）、不同自由度下χ2分布是我们进行卡方检验的必要元素。

具体怎么算？

（1）计算χ2值：

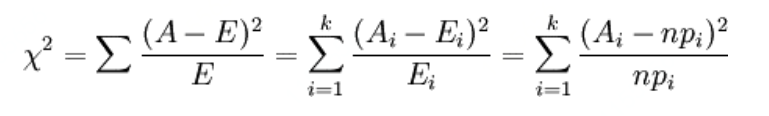
举个例子来说明公式的含义：

1）将高低CTR的广告图设计因素不同水平的数据呈现为列联表形式。

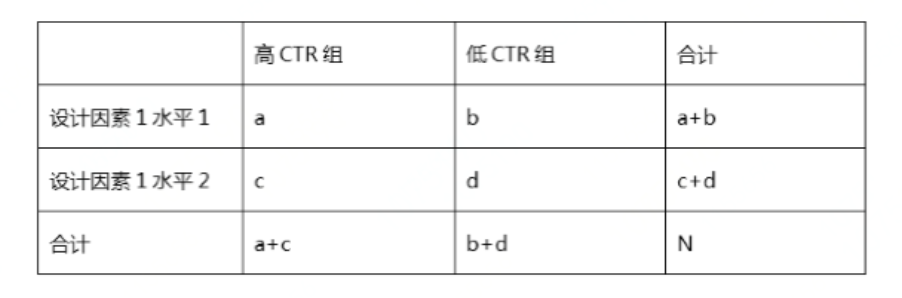
2）公式中A代表观察值，E代表理论值，（A-E）代表观察值及理论值的差异，其中理论值是假设两个因素无关的情况下计算出来的。

e.g. 设计因素1水平1×高CTR组的理论值即（a+b）×（a+c）/N

3）求平方和以避免正负差值间抵消：由于有多个观察值，差值可能出现正负值而互相抵消，故利用平方的计算来避免。

4）除以理论值以避免理论值大小影响偏差。

（2）确定自由度（df）

自由度指计算某一统计量时，取值不受限制的变量个数。在列联表中，由于行或列总数一定，因此行或列中受限制条件数为1，列联表总df=（行数-1）×（列数-1）。

e.g. 2×2列联表中df=1，在3×2列联表中df=2

（3）结合df及p值确定χ2分布中的临界值，与计算所得χ2值比较

e.g. df=1，p值为0.05情况下，χ2临界值为3.84

如果我们计算所得的χ2值＞3.84，意味着H₀假设落入了下图所示的右侧“小尾巴”似的拒绝域，H₀假设就不成立，即设计因素1不同水平下高低点击率广告图频数与平均频数有区别，换句话说，设计因素1的不同水平与高低点击率有相关。

spss怎么操作？

除了手工计算及查表外，可通过spss来进行卡方检验，步骤如下：

（1）导入数据

将每张广告图的高低CTR分组作为A列，设计因素1分组作为B列，导入spss作为原始数据，如下图框1所示。（若原始数据是上方表格的频数数据，需进行频数加权处理）

（2）选择<分析>-<描述统计>-<交叉表>

如下图框2所示：

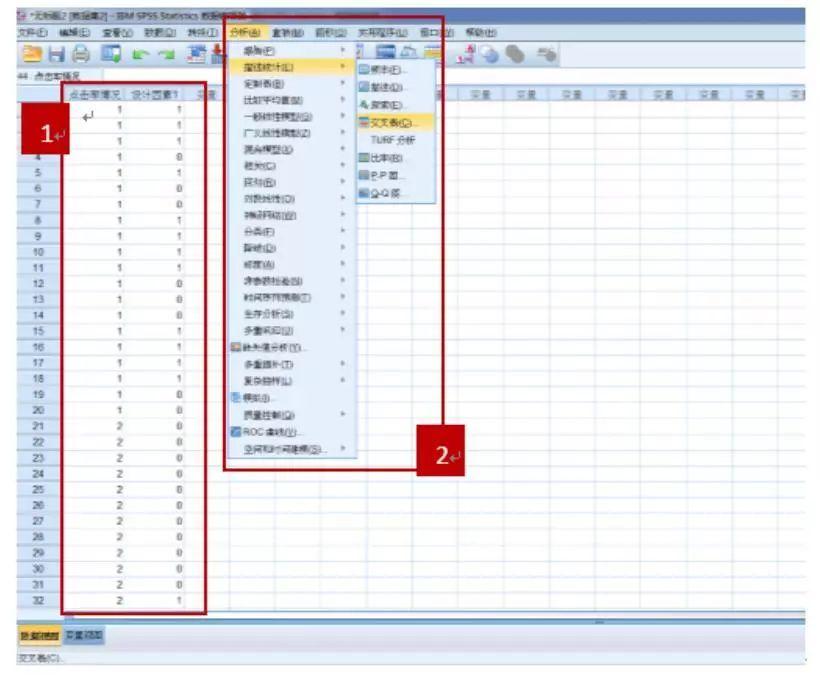
（3）将变量添加到行列中

在<统计>对话框中勾选卡方，在<单元格>对话框中勾选<z-检验>下方俩选项以便进行多变量间的两两比较。

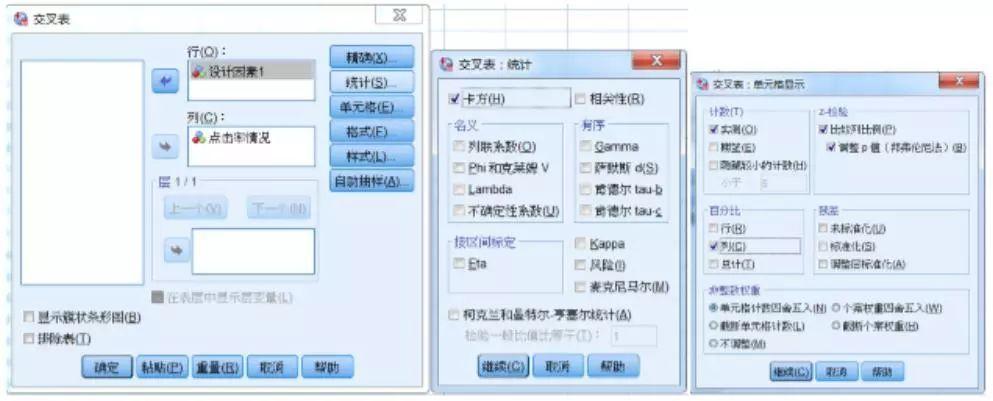
两两比较方法之Bonferroni法（邦弗伦尼法，修正最小显著差法）：在每次比较中，将显著性水平α除以两两比较的次数N，使得显著性水平缩小到原来的N分之一，降低α错误的概率，避免在原假设为真时拒绝原假设，没有显著差异却认为有显著差异。与常规的两两比较LSD检验（最小显著差法，Least Significant Difference）相比，其采用更严格的标准，更容易导致两两比较时无显著差异。

（4）解读结果

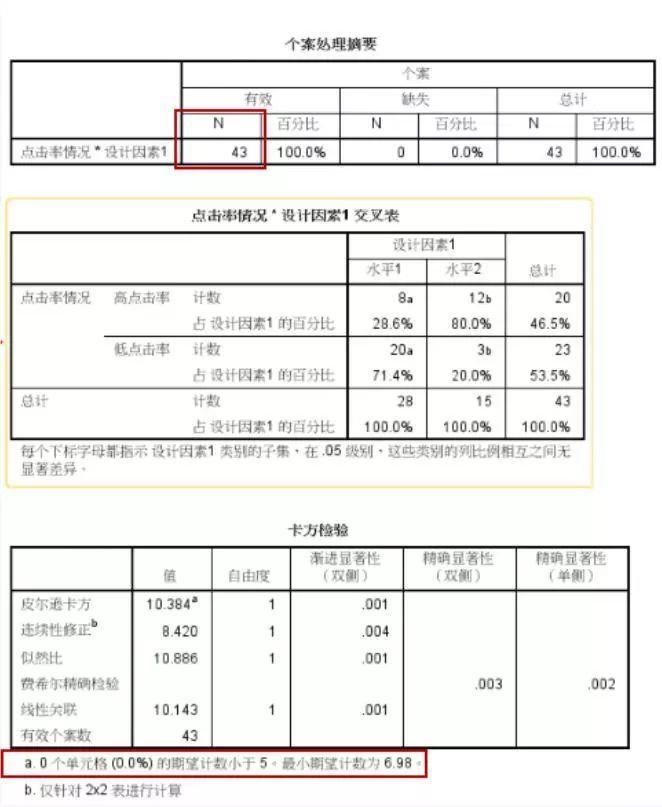
1）重点关注第三张卡方检验表格，指标的选择依照以下条件（定义n为总样本量，理论频数T）:

1. n≥40，T＜5的单元格未超20%，且T均＞1（图中展示符合此条件），采用皮尔逊卡方检验结果。e.g. χ2=10.38，p=0.001<0.05，即设计因素的不同水平会影响点击率情况，结合描述统计判定水平2的高点击率概率高于水平1。
2. 若行、列变量较多， n＜40，或有T＜1，采用似然比卡方检验。
3. 若是2×2的四格表，n≥40，1≤T＜5的单元格超20%，采用连续性修正检验结果。
4. 若是2×2的四格表，n＜40，或有T＜1，采用费希尔精确检验结果。
5. 若行、列量变量是等级变量（可从小到大排列）时，采用线性关联检验结果。

2）在确定初步结果显著之后，若列联表达到3列及以上，需两两比较列变量水平间是否有差异。第二张交叉表表格中有a、b的下标提供了比较结果，不同下标的列变量水平之间有显著差异。

结论不符合预期时，卡方检验结论如何解读？

至此完成了卡方检验的基本操作，但检验结果仅代表数据的显著性，该显著性是否有意义仍需要结合实际情况来看。当数据显著性出现与假设、预期不相符时，多是以下几种情况。

1. 描述统计差异较大但卡方检验不显著

e.g. 某品类广告的<商品图数量>元素，描述结论发现“两个”商品图的图片高于平均水平（高点击率图片整体比例）11%，但卡方检验却没有显著（χ2=6.79，p=0.08）。

这里就涉及到自由度的概念，由于<商品图数量>原始数据分类有四个水平：“无、一个、两个、三个及以上”，导致自由度增加，卡方分布由陡峭变成缓坡，拒绝域随之右移，需要更大的卡方值才能拒绝零假设，虽然例子中6.59＞3.84（自由度为1的极限卡方值），但仍＜7.82（自由度为3时的极限卡方值），因此判定该设计因素不同水平对高低点击率没有显著影响。

2. 描述统计差异不大但卡方检验显著

同样是多水平条件的卡方检验，可能导致另一种现象，某一水平下点击率情况与总体平均水平差异不大，但卡方检验显示其与高点击率相关。

e.g. 某品类<装饰元素>共三个水平“纯色、少量、复杂”，其中“复杂”水平下高点击率（32.5%）与整体平均水平（29.7%）差异并不大，但整体卡方检验显著，并将“纯色”、“复杂”两个水平认为与高点击率相关。

除“复杂”水平外其他两组分布与理论频数差异较大，导致整体的卡方分布显著，而事后进行两两比较的时候，“复杂”水平下频数表现与“纯色”组更为接近，因此“复杂”水平被认为与高点击率相关。

3. 结论与常规认知不相符

在对广告图进行分析时，有一定的常规认知假设，如用户会更偏好“有利益点”、“有品牌标识”的图片，但当卡方检验显示两者对点击率无影响时，可尝试从以下维度去排查问题。

（2）是否分类方式出了问题？

e.g.<利益点>原分类方式：有具体数值或明确赠品为“有利益点”，其他为“无利益点”，卡方检验后此设计因素对点击率无影响。

考虑到用户在浏览广告图时，不一定有具体数值才是有利益点，“全场秒杀”、“直降”的文字也会吸引用户点击，后续将<利益点>分类方式调整为{“无”、“直降促销（文字或数值）”、“满减、买免等促销（文字或数值）”、“买赠或其他”}。卡方检验发现中间两类明确利益点的广告图均有较高点击率。

分类方式作为原始数据对检验结论影响巨大，在进行设计因素分类时应遵循用户认知广告图的方式，不局限于单纯的视觉展现形式，从内容、视觉形式等角度全面考虑。

（3）是否品类有其特殊性？

e.g. <是否有大促标识>这个因素，在其他品类中，卡方检验常得到“有大促标识”比“无大促标识”有更多“高点击率”图片的结论，但在手机品类下却未有显著差异。

仔细观察后发现，手机品类广告图的单品促销较为常见，与大促活动关联度不高，因此在手机品类广告图展现大促标识对点击率影响不大是可以解释的。

（3）是否采样方式出了问题？

e.g. <文案行数>因素在某品类下仅“两行文案”水平与“高点击率”相关，难以解释。

用户对广告图的利益点感知最强烈，所以选择了<利益点>因素作为代表，与<文案行数>进行交叉，看两因素是否相互影响。而后发现，两行文案广告图中更多是低点击率利益点，即不同文案行数的广告图利益点分布不一致，样本分布有偏。这也提示后期在验证时，利益点、品牌效应等作为影响用户点击广告图的最重要因子，应尽量在其他变量间保持一致的分布。

4. 分类数据是否有更好的分析方法？

受数据类型的限制，不得已采用了卡方检验，仅能进行单个设计因素内不同水平的对比，无法进行多个设计因素间重要性对比，也无法考虑不同设计因素间的交叉影响，综合确定CTR更高的设计组合。

那么分类数据有没有更深入的分析方法呢？曾经同事采用了联合分析方法，对广告图元素设计进行了数据探索。简要来说，联合分析可以把用户在购买决策中一系列的产品特征/价格考虑在内，综合评估后确定用户偏好的因素组合。

本文案例为什么不适用呢？

因为联合分析对数据样本的元素组合分布有一定要求，必须符合“均匀分散”、“整齐可比”的正交分布特征。本文案例中的卡方检验更多是初步探索，在后续投放广告图进行A/B Test时可采用正交设计来确定不同设计因素组合，回收数据后采用联合分析明确最优广告图形式。

作者： 韩泱泱，京东设计中心JDC

来源：https://mp.weixin.qq.com/s/rf1ME045WoyEyQrTFp5coQ

本文由 @京东设计中心JDC 授权发布于人人都是产品经理，未经作者许可，禁止转载

题图来自Unsplash，基于CC0协议