100种分析思维模型之:统计思维
本文将带你了解统计思维的重要性和应用,通过深入浅出的案例分析,帮助你在数据分析的海洋中找到指路明灯,希望对你有所帮助。

你好,我是林骥。在信息爆炸的时代,不同的信息获取方式,可能让我们会产生不同的判断和决策。
究竟什么是真?什么是假?什么是有益的?什么是有害的?
下面介绍 100 种分析思维模型的第 71 种:统计思维,它能帮助我们揭示数据背后隐藏的规律和趋势,进而做出更加科学的判断和决策。
一、为什么学习统计思维?
我们大多数人都是感性动物,常常会因为情感而改变自己的想法,而难以时刻保持理智的判断。
比如,在选购一款商品的时候,假设有高档、中档、低档 3 种不同的型号,对应高、中、低 3 种不同的价格,大多数人都会选择中档,因为人们通常会有「回避极端」的心理。
通过学习统计思维,将数据与实际相结合,就可以在面对不确定性时,更加客观地分析信息的真伪,获得更有价值的信息,进而做出更加合理的判断和理性的决策。
假设你拥有统计思维,想要知道某款产品的市场表现,就可以分析相关数据,了解产品的销售情况、受众特征和销售趋势等,进而调整相应的销售策略,以便提升销售的业绩。
但是,假如你缺乏统计思维,就有可能仅凭直觉或主观判断做出决策,导致陷入盲目和错失发展机会的境地。
总之,统计思维可以帮助我们更加客观、理性地看待问题,从而做出更加明智的决策。
二、什么是统计思维?
统计思维是一种基于数据和概率的思考方式,通过统计数据并对其进行分析,进而更好地理解现状、分析原因和预测未来。
下面简单介绍一些统计学的核心概念,它们是统计思维的基础。
① 总体与样本
总体是统计研究的整个集合。例如,我们要研究中国人的平均身高,那么所有中国人就是总体。
样本是从总体中抽出的一个代表子集。例如,从中国人中随机抽取 1000 个代表来测量身高,这 1000 个人就是样本。
② 概率与频率
概率是某一事物发生的可能性。例如,抛硬币出现正面的概率是 50%。
频率是指在 N 次试验中,某一事件出现的次数 m 与 N 的比值。例如,抛了 100 次硬币,出现 51 次正面,那么出现正面的频率是 51%。
③ 参数与统计量
参数是描述总体特征的数值。例如,总体均数、总体标准差、总体相关系数等。
统计量是通过样本数据计算出来的数值。例如,样本均数、样本标准差、样本相关系数等。
统计学的概念还有很多,在此不做一一介绍,感兴趣的朋友,可以参考统计学的相关书籍。
统计思维侧重于「道」的层面,而具体的统计方法侧重于「术」的层面。无道之术,就像脱缰的野马,一路狂奔却没有方向。只有用道去驾驭术,才能取得更好的效果。
三、怎么运用统计思维?
统计思维是为了解决实际问题而产生的,无论是在工作中,还是在日常生活中,统计思维都能为我们提供有力的支持。
在运用统计思维解决问题的时候,我们可以先随机抽取一些样本,并尽可能让样本能够代表总体,然后找到与数据匹配的思维模型。
这个过程就像福尔摩斯探案,事先并没有确切的结论,只能努力先去寻找线索和证据,最后才能让案件真相大白。
比如,为了用更低的成本,及时了解中国人口的变化情况,统计局可以选取中国人口的 1‱ 进行抽样调查,通过抽样数据来预估中国人口的变化。
统计思维不仅可以解决一些数字相关的问题,而且能够解决一些看起来与「数」无关的问题。
比如,有人使用词频统计、回归分析、多重检验等统计学的方法,对《红楼梦》前 80 回和后 40 回进行对比分析,发现前后存在巨大的语言差异。
其中常用形容词、副词、虚词出现的频率,以及段落长度、分句、标点符号等,都发生了显著的变化。而一个人前后用语、用词以及标点符号的习惯,通常不会发生太大的变化。因此可以推断,《红楼梦》前 80 回和后 40 回的作者大概率不是同一个人。
与统计思维有关的正态分布、幂律分布、泊松分布、相关分析、假设检验等,都可以用来解决一些实际的问题。
很多人每天都在努力工作、学习和运动,但是为什么却看不到效果?
有一种 Sigmoid 函数,能够直观反映努力与成果之间的关系。
Sigmoid 函数的定义如下:
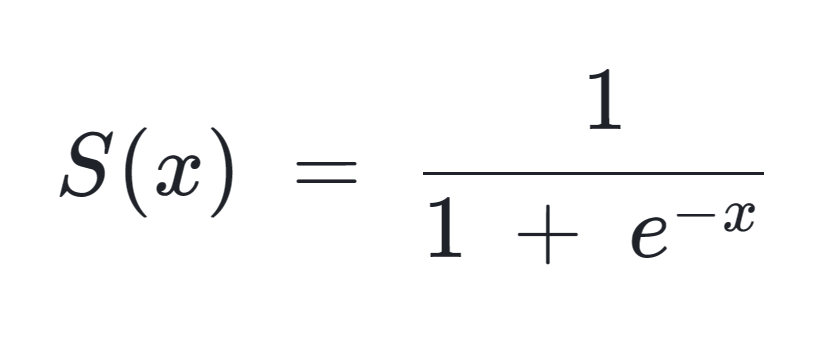
该函数对应的图形就像一个大写的 S 形,刚开始的时候处于停滞期,努力几乎不会产生什么成果,但是持续努力一段时间,到达某种程度之后,就能获得快速成长,甚至产生质的飞跃。
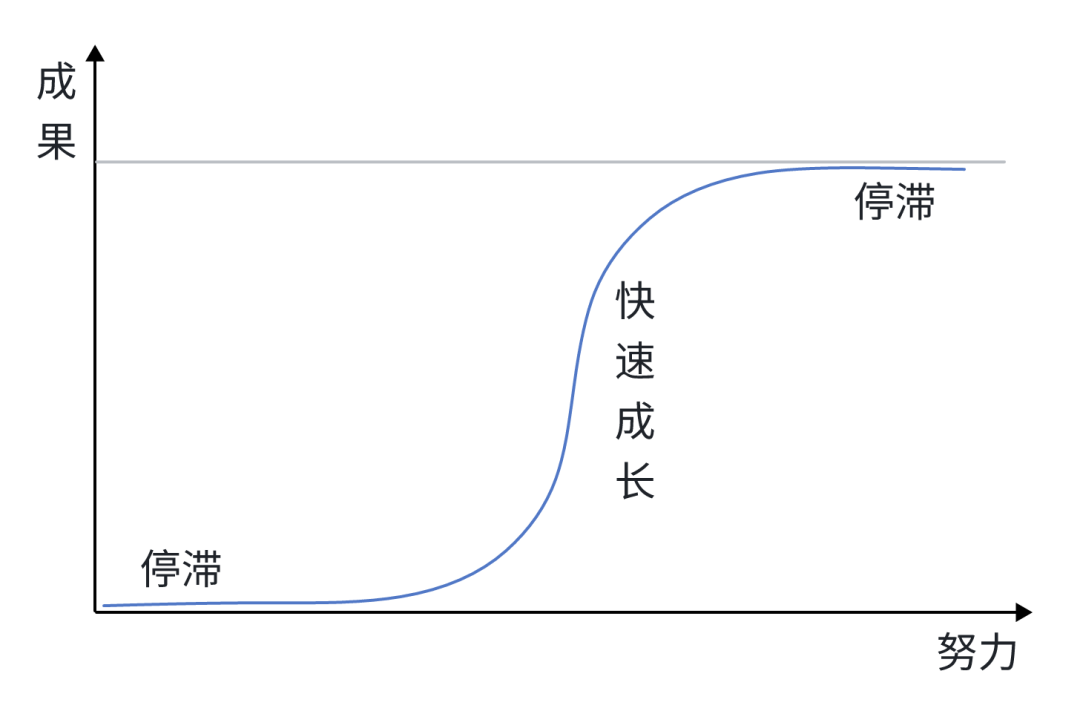
当努力变得艰难的时候,不妨想一想 S 型增长曲线,也许就会产生继续努力的动力。
在瞬息万变的世界中,如果我们运用统计思维,提升预测未来的能力,就更容易把握先机,提前做好的准备,并采取相应的行动。
但是,假如你的预测模型不对,或者初始条件不一样,就有可能导致「差之毫厘,谬以千里」。
比如,有一个简单的数学模型:y = 100 ^ x,也就是 100 的 x 次方。当 x = 1 时,y 等于 100,而当 x = 2 时,y 等于 10000。虽然初始条件 x 仅相差 1,但是结果 y 却相差了 100 倍,差距非常悬殊。
20 世纪 60 年代,气象学家爱德华·洛伦兹提出了「蝴蝶效应」,就是在一个复杂系统中,哪怕一个微小的变化,都有可能引起巨大的连锁反应。
所以,我们在运用统计思维的时候,一定要注意提高警惕。
在《拼凑真相》这本书中,作者蒂姆·哈福德介绍了认清纷繁世界的 10 大数据法则,这些数据法则能够帮助我们提升洞察事物本质的能力。
随着 AI(人工智能)技术的发展,我们可以快速处理和分析海量的数据。然而,统计思维的主角依然是人,因为最终还是需要靠人来对数据进行解读和运用。
四、最后的话
在用统计思维解决实际问题的时候,我们可能还会面临 3 大难题。
① 总体是谁?
在现实生活中,总体往往是难以确定和度量的。
比如,怎么统计人类的智力水平?这是一个动态变化且难以度量的问题。
但总体往往又非常重要,因为它就像是大海航行的灯塔,指明了解决问题的目标和方向。
② 数据从哪里来?
在大数据时代,虽然我们并不缺少数据,但是要想获得真正有价值的数据也不容易。
比如,怎么统计每个人的时间分配?这涉及到时间的记录、分类等操作,面临着准确性和及时性的挑战。
只有拿到正确的数据,才有可能得出正确的结果。
③ 结论到那里去?
这里的结论,并不是一个简单的统计结果,而是要把统计结果与现实问题紧密地联系起来,获得真正有价值的洞察。
然而,在现实世界中,统计结果很有可能与现实情况并不一致。
面对以上难题,我们该怎么办呢?
首先,我们要有用数据化解难题的意识,不要轻易做出判断。
其次,我们可以运用统计思维,获得化解难题的思路,不妨先大胆提出假设,然后再小心进行求证,严格按照统计学的流程规范,确保获得正确的结论。
最后,我们要理论联系实际,结合具体领域的知识背景,提升自己对业务的理解和认知水平,进而更好地解决实际的问题。
人生是由一系列选择组成的,我们每天都要做出各种各样的选择,从早上几点钟起床,到早餐吃什么,再到一天的时间怎么安排,以及晚上几点钟睡觉等等。
基于统计思维做出的选择,通常都会比随意选择得到的结果要好得多。
学会运用统计思维,就像拥有一种透视镜,让我们能够透过表面的现象,看到事物背后的规律和趋势,进而做出更加睿智的决策。
公众号:林骥,《数据化分析》作者
本文由 @林骥 原创发布于人人都是产品经理。未经作者许可,禁止转载。
题图来自Unsplash,基于CC0协议。
该文观点仅代表作者本人,人人都是产品经理平台仅提供信息存储空间服务。
- 目前还没评论,等你发挥!


 起点课堂会员权益
起点课堂会员权益






