知识点掌握度评估方法(一) — IRT
在教育测评领域,掌握度评估正从“分数导向”走向“认知建模”。本文以IRT(项目反应理论)为核心,系统解析其建模逻辑、参数含义与应用场景,帮助产品人理解如何通过数据驱动实现更精准的知识评估。

一家优秀的在线教育企业,除了在商业模式上具有一定优势外,其核心还是教育质量与效果,传统评估教育质量与效果是通过做题正确率、学习时长等参数作为教学效果的体现,但这样的做法比较粗糙,存在很大的误差。项目反应理论(IRT)作为教育效果测量领域的核心模型,通过量化学生能力与题目特性的关联,为在线教育知识点掌握度评估提供更加精准、科学的解决方案。本文将从公式推导、参数意义、应用场景三个维度,对 IRT 模型进行深度解析。
一、IRT 模型的公式推导
IRT 模型的推导建立在一系列核心假设之上,这些假设是模型有效性的基础,同时也决定了其在在线教育场景中的适用边界。
1. 核心假设
单维性假设:
假设学生对某一知识点的作答表现,仅由 “该知识点的掌握能力” 这一单一潜在特质决定,不受其他无关因素(如答题情绪、外界干扰)等影响。这一假设贴合在线教育中 “针对性评估单一知识点” 的需求,例如评估学生对 “一元二次方程求根公式” 的掌握度时,仅聚焦该知识点的能力维度。
局部独立性假设:
学生对不同题目(同属同一知识点)的作答反应相互独立,即对一道题的作答结果不会影响另一道题的作答。在线教育中,同一知识点的题库设计常遵循此假设,避免题目间存在逻辑关联导致评估偏差。
特征曲线假设:
学生答对某道题的概率,随其知识点掌握能力的提升而单调递增,即能力越强,答对概率越高,这一关系可通过 “项目特征曲线(ICC)” 呈现。
2. IRT公式
IRT 公式一共有以下参数:θ(学生能力值/知识点掌握度)、题目区分度a(能够区分学生能力强弱)、题目难度b()、题目猜测参数c(能力为0也可以猜对的概率),根据参数数量可分为1PL模型(Rasch 模型)、2PL模型、3PL模型,在线教育中常用双参数与三参数模型。3PL模型的公式如下:
P(θ):此习题的答对概率;
D(常数 1.702): 用于校准概率尺度,使 Logistic 模型与正态卵形模型(Lord 模型)近似,提升计算效率。
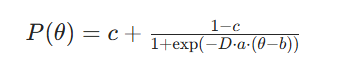
1.学生能力参数 θ
θ 是 IRT 模型的核心输出,直接对应学生对某一知识点的掌握度,具有以下关键意义:
- 精准量化与横向对比:θ的取值([-3,3])可将“掌握度”从模糊的“会/不会”转化为精准的数值。例如,学生A的θ=1.2,学生B的θ=0.5,说明A对该知识点的掌握度显著高于B,且差值可量化,避免传统“正确率相同但能力不同”的偏差(如A答对难题,B答对易题,正确率均为80%,但θA>θB)。
- 动态追踪能力变化:在线教育中,可通过学生在不同时间点的θ值,追踪其知识点掌握度的提升或下降。例如,学生在课程开始时θ=-0.3,课程结束后θ=1.1,说明教学有效提升了其掌握度,为教学效果评估提供直接依据。
2.题目难度参数 b
b 与 θ 同量纲,其意义在于为在线教育题库的 “分层设计” 提供标准。
- 题库难度梯度划分:将题目按b值分为“基础题(b≈-1)”“中档题(b≈0)”“难题(b≈1)”,匹配不同θ值的学生。例如,对θ=-0.8的新手学生,推送b≈-1的基础题,避免因题目过难导致挫败感;对θ=1.5的进阶学生,推送b≈1的难题,满足其提升需求。
- 知识点难度校准:通过大量学生的作答数据,计算某一知识点下所有题目的平均b值,可判断该知识点的整体难度。例如,“微积分导数应用”的平均b=1.2,“小学数学加法”的平均b=-1.5,为课程设计(如“微积分”需更多课时)提供参考。
计算方式(经典测量理论)
最常用 “通过率(P 值)” 表示(,P =答对该题的学生人数/参加测试的总学生人数
- P取值范围:(0=<P<=1);
- P越接近1:题目越简单。
- P越接近0:题目越难,如超纲的大学物理题给初中生做,P≈0)
初始化方式
存在大量历史数据:按照经典测量理论。
极少/没有历史数据:预设难度
3.题目区分度参数 a
a 决定了题目对不同掌握度学生的区分能力,是在线教育题库 “质量筛选” 的关键:
- 优质题目的核心标准:在线教育中,优质题目需具备较高的a值(通常a>0.8)。例如,a=1.2的题目,能清晰区分θ=0.5与θ=1.0的学生(前者答对概率50%,后者答对概率80%);而a=0.3的题目,对这两类学生的答对概率差异仅为10%,区分能力弱,应从评估题库中剔除。
- 针对性评估场景适配:在“知识点掌握度诊断”场景中,需选择a值较高的题目,确保能精准定位学生的能力区间;在“巩固练习”场景中,可适当降低a值要求,重点关注知识点的熟练度而非区分度。
计算方式(经典测量理论)
最常用 “点双列相关系数r(pb)”:通过计算 “学生在该题的得分(0/1)” 与 “学生的测试总分(代表整体能力)” 的相关性,判断题目能否区分能力:
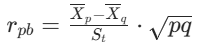

没有历史数据如何确认a和b
经典测量理论(CTT)、专家经验、小规模试测和IRT 模型简化应用相结合的方法,可逐步确认习题的难度、区分度和猜测参数。
4.猜测参数 c:评估偏差的 “修正因子”
c 主要用于修正选择题等存在猜测可能的题型的评估偏差,其意义体现在:
- 排除猜测对能力评估的干扰:传统正确率计算中,学生靠猜测答对的题目会被计入“掌握”,导致θ值高估。例如,某学生θ=-1.0(完全未掌握),做4个选项的选择题时,猜测正确率25%,传统评估会认为其掌握度25%,但IRT模型通过c=0.25修正,计算得实际θ仍为-1.0,避免偏差。
- 题型适配调整:对于主观题(如简答题、编程题),学生几乎无法猜测,可设c=0,采用双参数模型;对于选择题、判断题,需根据选项数量设定合理的c值(如判断题c=0.5),确保模型贴合题型特性。
3. IRT公式不同参数公式
1. 1PL模型(Rasch 模型)
应用场景:题目区分度一致的标准化测试。 去掉a和c参数。
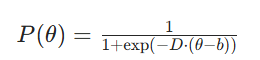
单参数模型仅包含 “题目难度” 一个题目参数,核心表达式基于逻辑斯蒂函数推导:
- 首先,定义核心变量:设θ为学生的知识点掌握能力(潜在特质,取值范围通常为[-1,1],值越大能力越强);b为题目难度参数(取值范围同θ,值越大题目越难)。
- 学生答对某题的概率P(θ),本质是“学生能力与题目难度差值”的函数。当θ=b时,学生答对概率为0.5,符合“能力与难度匹配时,答对概率居中”的直觉;当θ>b时,P(θ)>0.5,能力越强概率越高;当θ<b时,P(θ)<0.5,能力越弱概率越低。
- 基于逻辑斯蒂函数的单调性与“S型曲线”特性(贴合答题概率随能力变化的实际规律),推导得单参数模型公式:
2. 双参数模型
应用场景:无序考虑c猜测的场景,例如主观题、简答题、填空题等。去掉c参数
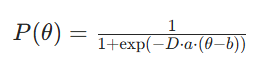
单参数模型未考虑 “题目区分度”(即题目对不同能力学生的鉴别能力),双参数模型在其基础上增加 “题目区分度参数 a”,推导过程如下:
- 定义a为题目区分度参数(a>0,值越大,题目对不同能力学生的区分能力越强,例如一道区分度高的题,能力强的学生几乎必对,能力弱的学生几乎必错)。
- 区分度a通过调节“能力与难度差值”的权重,影响概率曲线的陡峭程度:a越大,曲线在θ=b附近越陡峭,说明题目在“能力接近难度”的区间内,能更精准区分学生能力;a越小,曲线越平缓,区分能力越弱。
- 基于单参数模型扩展,推导得双参数模型公式:
3. 三参数模型
应用场景:选择题场景
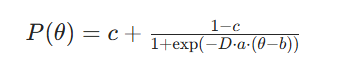
在线教育中,学生可能存在 “猜测作答”(如选择题随机选答案)的情况,三参数模型增加 “猜测参数 c”(0 ≤ c ≤ 0.25,常见选择题为 4 个选项,最大猜测概率为 0.25,如果是5个选项,则最大猜测概率为0.2,如果是多选题,是另外的算法),推导如下:
- 定义c为学生完全不具备该知识点能力时(θ→-∞),仍能答对题目的概率(即猜测概率)。
- 当θ→+∞时,学生能力极强,答对概率趋近于1;当θ→-∞时,答对概率趋近于c,贴合实际答题场景。
四、θ知识点掌握度如何确定?
上面的公式讲的都是正向推导模式,那么有了习题的做题数据了,如何反推θ值呢,首推的是MLE极大然估计方法。
步骤:
- 假设学生能力θ服从正态分布;
- 筛选过往针对知识点的习题数据;
- 构建似然函数
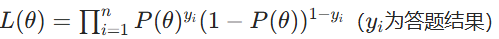 答题正确y_i=1,答题错误y_i=0;
答题正确y_i=1,答题错误y_i=0; - 对θ取对数并求导,找到使对数似然最大的θ值。
本质:
当θ值为多少时,用户答题结果概率最大会是这样,例如{1,1,0,1,1}.
五、IRT 模型的应用场景:赋能在线教育效果评估与产品优化
IRT 模型并非理论工具,而是能直接落地于在线教育产品的核心功能,解决传统评估的痛点,主要应用场景包括以下三类:
1. 个性化题库推荐:实现 “千人千题” 的精准练习
在线教育的核心需求之一是 “因材施教”,IRT 模型可通过 θ 与 b 的匹配,实现个性化题库推荐:
- 推荐逻辑设计:基于“最近发展区”理论,推荐b值略高于学生当前θ值(通常b=θ+0.3~0.5)的题目。例如,学生θ=0.8,推荐b=1.1~1.3的题目,既避免因题目过易导致“无效练习”,也避免因过难导致“挫败感”,确保练习效率最大化。
- 动态调整推荐策略:随着学生作答,实时更新θ值,并同步调整推荐题目难度。例如,学生连续答对3道b=1.2的题目,θ提升至1.0,推荐题目难度调整为b=1.3~1.5;若连续答错2道,θ降至0.6,推荐难度回调至b=0.9~1.1,实现“动态适配”。
- 实际产品案例:某K12在线教育产品的“智能题库”模块,基于IRT模型为每个学生生成“能力-难度匹配曲线”,推荐题目正确率稳定在60%~70%(对应b=θ+0.4),用户练习后知识点掌握度提升速度较传统“随机推荐”快30%。
2. 学生知识点能力诊断:生成 “精准能力画像”
传统评估仅能给出 “正确率”,而 IRT 模型可通过 θ 值与题目参数的关联,生成学生的 “知识点能力画像”,助力教师与学生定位薄弱环节:
- 能力区间定位:将θ值划分为“未掌握(θ<-1)”“初步掌握(-1≤θ<0)”“熟练掌握(0≤θ<1)”“精通(θ≥1)”四个区间,明确学生当前所处阶段。例如,学生θ=-0.5,定位为“初步掌握”,需重点巩固基础概念;θ=1.2,定位为“精通”,可进行拓展学习。
- 薄弱点细化分析:通过学生对不同b值、a值题目的作答情况,定位具体薄弱点。例如,某学生对“一元二次方程”知识点的θ=0.3,但对b=1.0的“含参数一元二次方程求解”题目答对率仅20%,说明其在“含参数问题”这一细分薄弱点需加强。
- 诊断报告输出:在线教育产品可基于IRT模型生成“知识点能力诊断报告”,包含θ值、能力区间、薄弱点列表、推荐学习内容等,例如:“您对‘几何证明’的掌握度为θ=0.2(熟练掌握),但在‘全等三角形辅助线添加’(b=0.8)题目中表现较弱,推荐学习‘辅助线添加技巧’专题课”。
3. 教学效果评估:从 “表面数据” 到 “本质效果” 的跨越
IRT 模型可突破传统 “学习时长、正确率” 的表面数据,从 “学生能力变化” 的本质维度评估教学效果,适用于课程、教师、班级的多维度评估:
- 单课程效果评估:对比学生在课程开始前(前测)与结束后(后测)的θ值变化,计算“θ提升量”(Δθ=θ后-θ前),作为课程效果的核心指标。例如,某“Python入门”课程,学生前测θ=-0.8,后测θ=0.5,Δθ=1.3,说明课程有效提升了学生的编程基础能力;若Δθ<0.2,需优化课程内容或教学方法。
- 教师教学效果对比:在同一课程、同一批学生的前提下,对比不同教师班级的平均Δθ值。例如,教师A班级平均Δθ=1.1,教师B班级平均Δθ=0.7,说明教师A的教学方法更有效,可将其经验提炼为“优质教学案例”推广。
- 知识点整体教学效果监控:统计某一知识点(如“初中物理力学”)所有学生的平均θ值与分布情况,判断整体教学是否达标。例如,若80%学生的θ≥0.5(熟练掌握),说明该知识点教学效果良好;若40%学生的θ<-1(未掌握),需重新设计教学方案,补充基础课程。
结语
在在线教育回归教育本质的趋势下,IRT 模型为知识点掌握度评估提供了科学、精准的解决方案。通过公式推导理解模型逻辑,通过参数解读明确核心指标,通过场景应用落地产品功能,IRT 模型可帮助在线教育产品突破传统评估的局限,真正聚焦 “教育质量与效果”,实现 “以评促教、以评促学” 的目标。未来,随着在线教育数据量的增长与模型算法的优化,IRT 模型将在个性化学习、智能教学决策等领域发挥更大价值,成为在线教育产品的核心竞争力之一。
本文由 @luffy 原创发布于人人都是产品经理。未经作者许可,禁止转载
题图来自 Pixabay,基于CC0协议
该文观点仅代表作者本人,人人都是产品经理平台仅提供信息存储空间服务


 起点课堂会员权益
起点课堂会员权益







请问目前工业界应用的教育个性化是使用的IRT吗,我看见技术也有一些深度知识追踪的模型,但是IRT感觉确实也更可控,更简洁。
可以加微信eyu1988810