如觉得证明过于复杂，可直接看文末总结的本游戏技巧。

——————

从表面上看，神经猫能走到的格子数是9×9=81格，但这个“棋盘”并不是对称的，神经猫只需要走4步就能到棋盘的边缘，而一旦被神经猫逃到棋盘边缘，游戏就结束了。

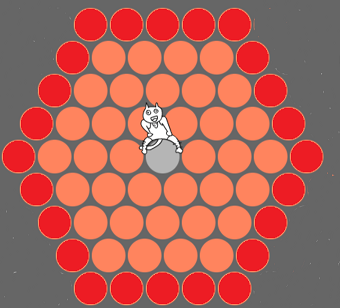
神经猫的逃跑策略是贪心算法，也就是说，它总是考虑当下离边缘最近的路线。实际上，如下图所示，神经猫4步可以走到的格子被深红色标出，其中带五角星的是棋盘的边缘。

神经猫显然会尽可能地往带五角星的格子逃跑，而我们要做的便是在猫到达五角星格子以前，把它拦住。

为了便于讨论，我们考虑更具有代表性的问题，如下图所示：

问题描述：在一个边长为M（上图中M=5）正六边形的棋盘上，要在最坏情况下，依然确保能抓住神经猫，令最小能满足条件的M为N，求N的值。

解：

本文给出N的上界，即。

引理：
在下图中，神经猫先行，它无法逃出。
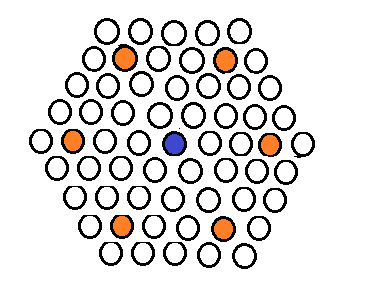经过穷举，这个结论是容易证明的，下图给出一种神经猫企图逃出却失败的例子：数字代表次序，蓝色的数字是神经猫的逃跑路线，橙色数字是我封堵的路线，请注意观察橙2、4、6、12的封堵技巧。显而易见，神经猫无法逃出。

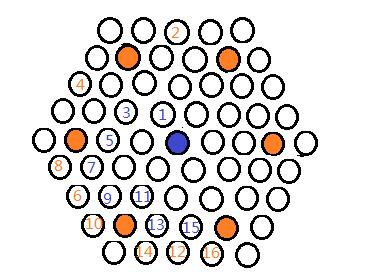
引理证毕。

下面证明N=8时，无论神经猫用什么办法，总存在策略将其围住。
只需证明，初始状态什么都没有的时候，依然可以围住神经猫即可（如下图所示）。

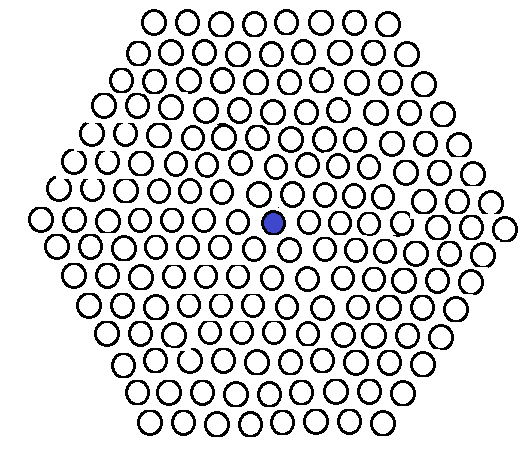
由于第一步之前，我们并不知道神经猫往哪个方向逃走，因此如果神经猫足够聪明，它显然会根据你的堵截方向，向反方向逃跑，因此第一步的阻拦的作用是微乎其微的。故作较坏打算：假设神经猫先行。

由对称性，不妨设神经猫第一步试图左上方逃走，于是如下图所示。

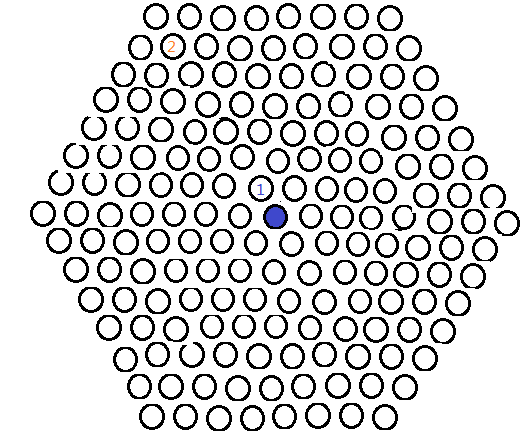
蓝1向左上行，橙2拦在了一个很远的地方，围棋十诀有云：慎勿轻速。虽然敌人看起来很遥远，但是还应该小心翼翼地渐渐靠近它，万万不可一开始就近身肉搏。

1）神经猫A是个楞头青，认为只要努力就能冲出重围，于是始终往左上跑

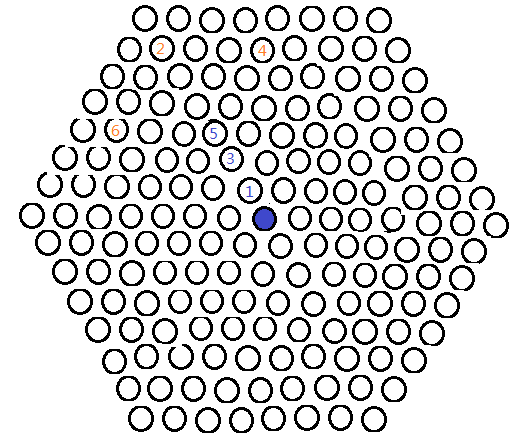
到橙6，由引理可知，神经猫已经无法从左上方逃走。
于是A企图转向，可是，如果它扭头就走——

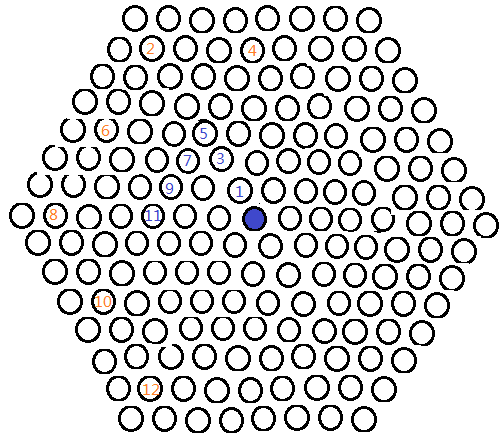
至橙12，我方已经占据了包围蓝方的有利地形，显然神经猫已经无法从坐下方跑出了，如果它想从其它位置出去，则显然更加不可能了。

如果A选择慢慢转向——

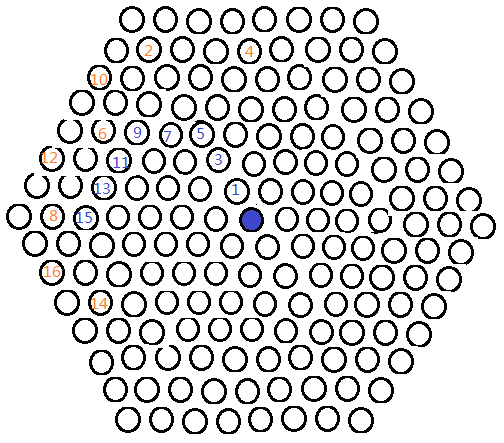
看起来似乎要逃出去了，但终究差一口气啊……
神经猫A，扑街。

2）神经猫B似乎聪明了很多，它会视情况，选择性地躲着敌人跑
看到橙2的堵截，B选择了躲避，往又上走，可惜，我方技高一筹，放在了橙4的位置，如下图所示——
至橙8，殊途同归，由引理知，神经猫B依然无法逃脱。

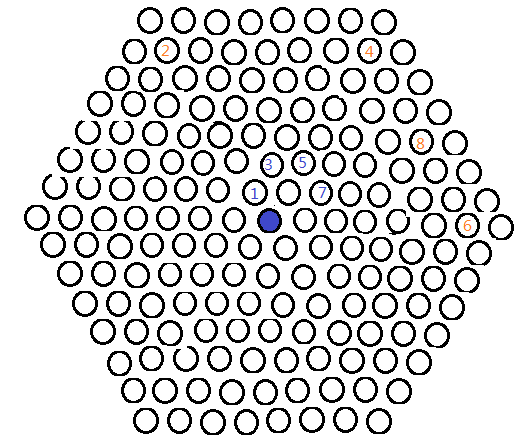
神经猫B，扑街。

3）神经猫C是一个谨慎的猫咪，它见到敌人，尽量躲避
如下图所示，蓝5很及时的转向，可是道高一尺，魔高一丈，橙6看似不着边际，其实上是张开了一张大网，至橙8，C已经无法逃出了。

神经猫C，扑街。

4）神经猫D是一个胆小的猫咪，它见到敌人，扭头就走
如下图所示，蓝3、5、7、9、11皆是躲着防线在跑，可是，至橙12，我方已经张开一个六边形的大网，等着D的到来，D终究要面对被擒的现实。

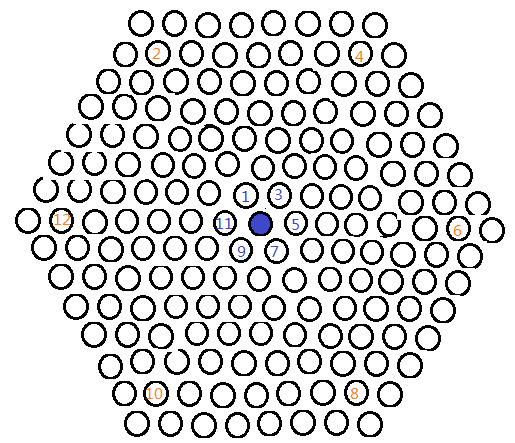
神经猫D，扑街。

于是，神经猫终究逃不出我的手掌心。
其实细心的你应该已经发现，我只要想办法尽快占据下图的紫色圈就可以确保擒住神经猫了。

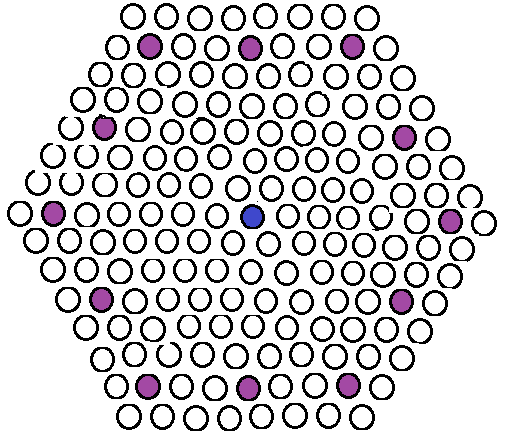
综上所述，得证。

——————————

回到原游戏。从上面的分析可以感受到“围住神经猫”的技巧精髓有如下几点：

1、慎勿轻速。除非有援兵，否则应该要远远地张开一张大网，在己方很弱的情况下，切勿轻敌。因为你的速度不比神经猫快，所以直接近身堵截，你总是慢一步啦。

2、“二间跳”是一个很实用的防御手段，如下图所示

当然，“二间跳”后的“双飞燕”也是很重要的，这样就彻底守住了。如下图所示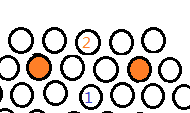
3、由于游戏中神经猫比较笨，它在左上方有通道的情况下会一味地往左上方逃跑，而不会拐弯，所以，在左上防御充分的前提下，还是尽可能在其它位置做好防御，防患于未然嘛。

4、上面已经说了，当N=8的时候，我才能确保捉住神经猫，对于本题来说，相当比N=5略好一些，确实有些情况，因为自己子力太弱，自己根本无法捉住神经猫——这个时候，就放小猫咪一个生路好了，它很可怜的啦。

另外，用X步 击败（100-X）%的人 的这个计算方法还是第一次见到 有点逗 ，很能引爆朋友圈！

原文作者：曾加@知乎

本文由人人都是产品经理@边缘 整理自知乎回答，转载请注明并保存原文链接！