编辑导语：数据分析对于用户调研来说十分重要，本篇文章作者分享了有关结构比率归因、量化异常分析的内容，并且列举两个具体案例进行分析，一起来学习一下吧。

我们来看下面一个场景，表一是2020和2021年不同用户群体的用户数，以及对应群体的付费率。

表二是2020年和2021年总体的付费率下降了2.8%。想问一下，我们通过表一如何分析原因？

付费率= 付费人数/总人数

表一：

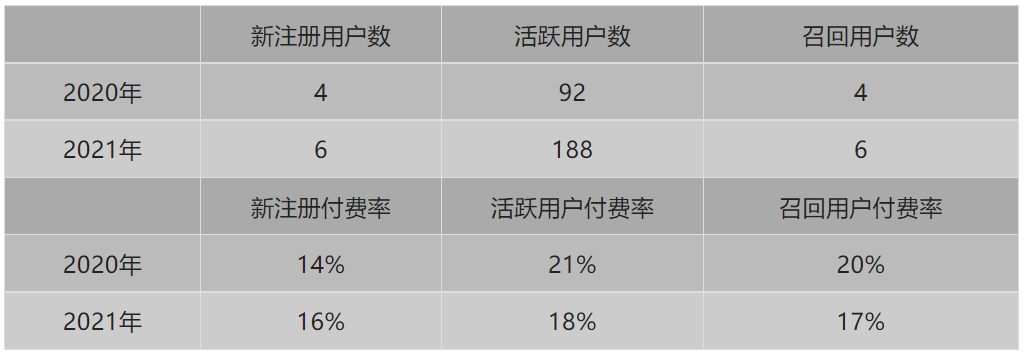
表二：

一、付费率下降原因定位

1. 结构占比变化

由上表一我们可以算出来各个用户群体，在2020年和2021年结构的占比，以及占比的变化：

表三：

2. 比率——付费率变化

由上表一我们又可以算出来各个用户群体，在2020年和2021年付费率的变化：

表四：

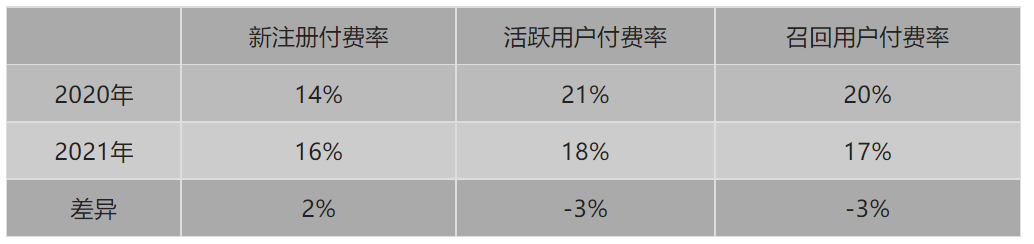
3. 整体付费率变化的贡献值

通过表三和表四，我们可以得到各个群体比率变动和结构变动对于整体付费率变化的影响大小，见表五：

表五：

总的付费率变动=0.07%+(-2.79%)+(-0.11%)+(-0.15%)+0.39%+(-0.19%)=-2.8%。

与上面表二的结果是一样的。

4. 结果解读

通过表五得出来的结果，我们可以看到总体付费率的变化是由于活跃用户付费率的下降，导致了整体付费率的下降。

那么，我们是如何得到表五的数据呢？

二、分析——结构比率问题

接下来是一段长文推导，如有不适，忍着看完，进行思考。

假设各群体的占比和付费率如下：

表六：

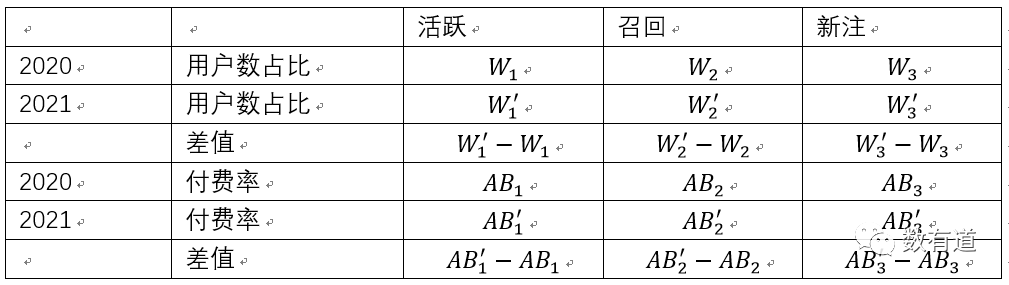
每一部分（群体）变动的计算：

比率(付费率)变动影响：公式1。

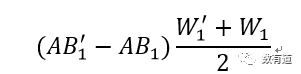
结构占比变动的影响：公式2。

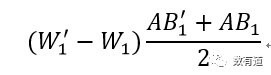
1. 如何理解

我们是希望把总的比率(付费率)变动分解为不同维度（用户群体）比率变动和结构占比变动，这样我们就能够方便的看出：

1. 到底是这个群体比率上升下降的原因，还是说这个群体的占比上升下降导致整个比率的上升下降；
2. 看整个比率变动的主要原因和次要原因，对其进行量化。

说完目标，接下来看看具体公式的理解。

2. 比率变动的影响

主要是量化活跃用户比率（付费率）的变化对于整体比率（付费率）变化的影响，我们使用AB1′-AB1，这是活跃用户比率变化的绝对量。

但是我们考虑的是对总体比率变化的影响，所以需要乘以活跃用户占比，但是活跃用户占比是在变化的，这里我们就直接乘以（W1′-W1）/2，使用均值来稳定占比的变化。

这样我们就计算出来了活跃用户比率变化对于整体比率变化的影响了。

3. 结构占比变动的影响

公式1仅计算出了活跃用户比率变化对于整体比率变化的影响，我们还需要考虑活跃用户结构的变化对于整体比率变化的影响，所以就有了公式2。

公式2的理解跟公式1一样，考虑活跃用户结构变化的绝对量，然后乘以稳定的比率。

单个群体（活跃用户）变动计算：公式3。

这样我们就能得到单个群体变动对于总体变动量：

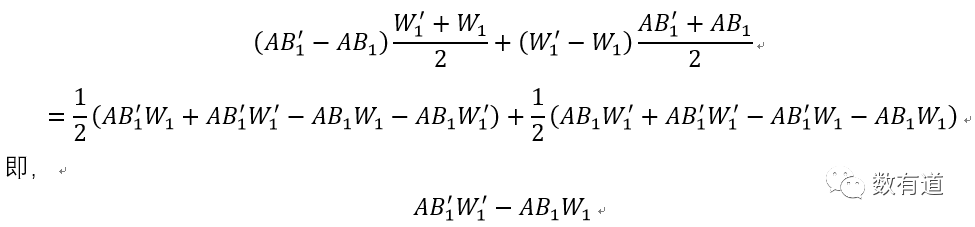
同理所有的变动就是各个群体变动相加：公式4。

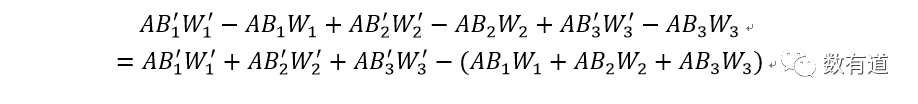
总体变动：

假设总体用户为a,则总体付费比率AB可表示为：公式5。

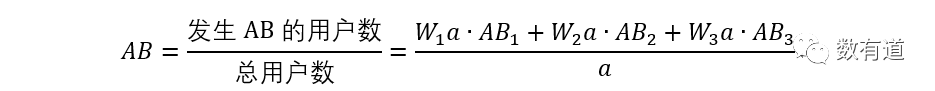
即：公式6。

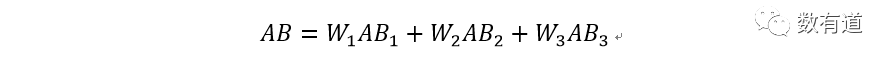
因此：公式7。

所以，总的比率（付费率）理论上就是等于各个群体的比率变动影响和结构变动影响相加。

接下来就是一个分渠道购买率定位问题的案例，以及对于辛普森简单理解。

三、案例1——分渠道购买率-定位三板斧

表七：

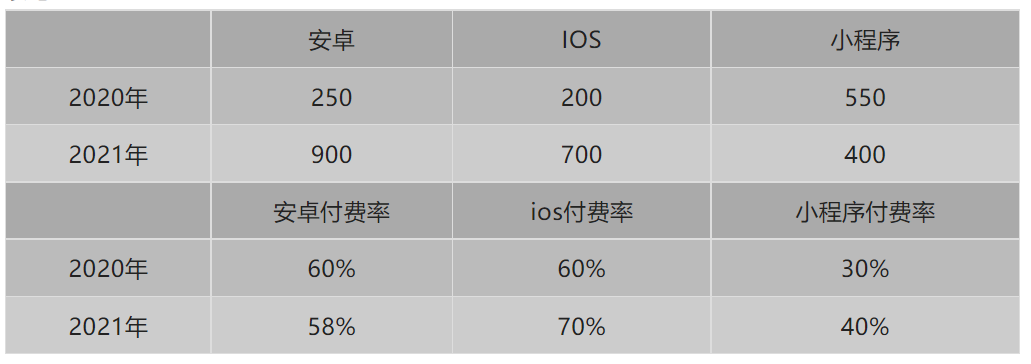
1. 算出每个群体比率和结构差值

表八：

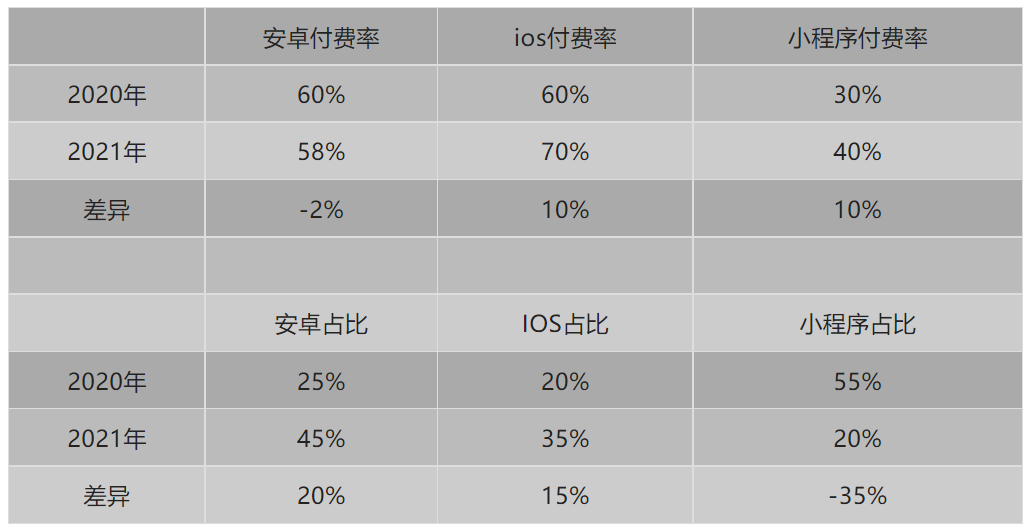
2. 计算每一个渠道的贡献

表九：

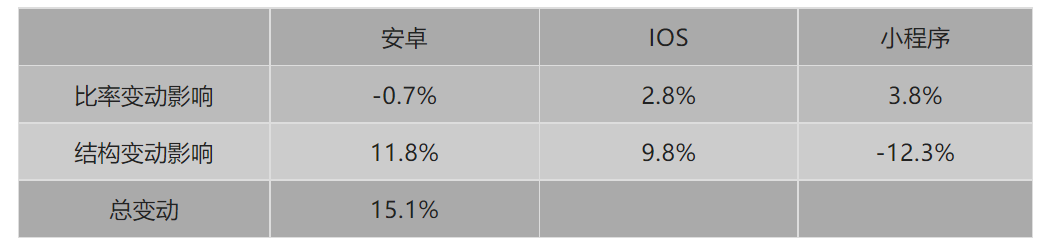
3. 单独计算总付费率

表十：

总结：

我们从表九可以看到：主要是由于安卓端占比的上升，以及IOS占比上升导致总体的付率从43.5%上升到58.6%

四、案例2——辛普森悖论的理解

什么是辛普森悖论：

当人们尝试探究两种变量（比如新生录取率与性别）是否具有相关性的时候，会分别对之进行分组研究。然而，在分组比较中都占优势的一方，在总评中有时反而是失势的一方。

例如表十一，总体的付费率是在上升，但是安卓和IOS的付费率都是在下降。

表十一：

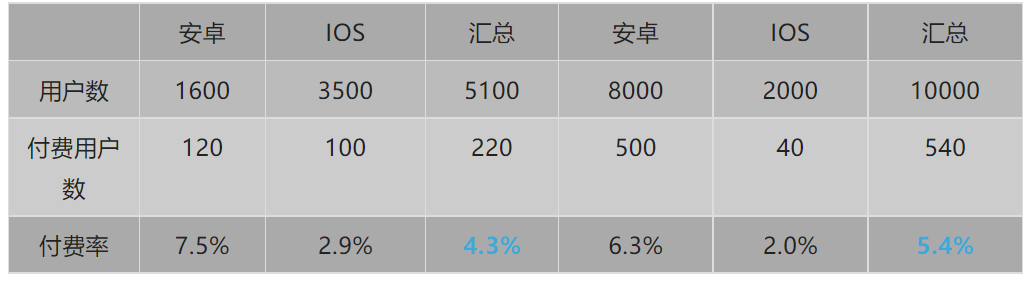
从表十一我们很快得到表十二的数据。

表十二：

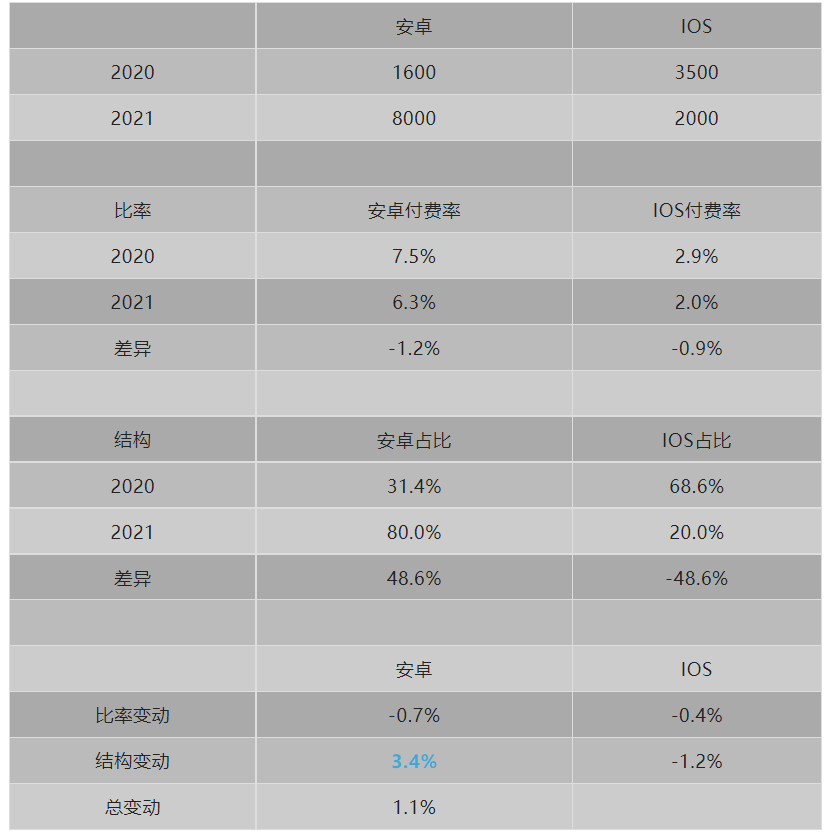
结论：从表十二，我们可以看出主要是由于安卓的占比上升导致整个付费率的上升。

写在最后：感谢怡然同学的合作和支持。

本文由 @数有道 原创发布于人人都是产品经理，未经许可，禁止转载。

题图来自Unsplash，基于CC0协议。