机器学习之K近邻算法基本原理
机器学习中的K近邻算法是一种基于实例的学习算法,有点像“人以类聚,物以群分”的说法。之前的文章很多都是说算法原理,这篇文章,我们来讲讲其优缺点和使用场景。
一、K近邻算法如何理解?
K近邻(K-Nearest Neighbor, KNN)是一种基于实例的学习算法,它利用训练数据集中与待分类样本最相似的K个样本的类别来判断待分类样本所属的类别。在机器学习中用于分类和回归分析。
二、K近邻算法的基本原理?
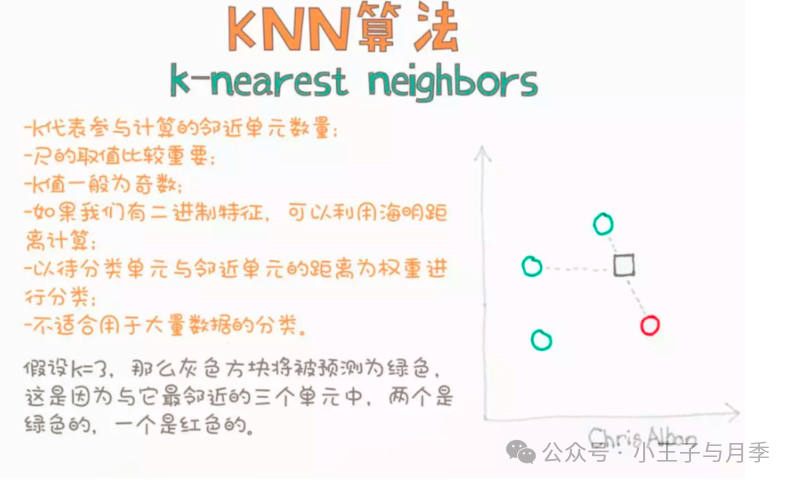
在训练数据集中找到与该实例最邻近的K个实例, 如果这K个实例的大多数都属于同一个分类,就把该输入实例分类到这个类中。一般情况下,我们只选择样本集中前K个最相似的数据,这就是K近邻算法中k的出处(通常K是不大于20的整数)。比如:比较3个最近的数据,那么K=3。
最后,选择K个最相似的数据中出现次数最多的分类,作为新数据的分类。
这种思想实际上也非常好理解,有点像“人以类聚,物以群分”的说法——如果你身边的邻居都来自同一个公司,那么你极有可能也属于某个公司;如果你身边的朋友绝大多数都属于某个学校毕业,那么你极有可能也曾经在这个学校读过书。
这种方式也很类似投票机制,新来的数据与旧数据相比对,多数都属于某个类别时,采用少数服从多数的原则,给新数据归类。
同样,我们转化到几何的方式去看这个算法,KNN可以看成:有那么一堆你已经知道分类的数据,然后当一个新数据进入的时候,就开始跟已知数据里的每个点求距离,然后挑离这个训练数据最近的K个点看看这几个点属于什么类型,就把这个新的点归到这个同属大多数的类别里。

三、K近邻算法的一些关键哪些?
1. 距离度量
KNN算法的核心在于距离度量,它决定了样本之间的相似度。通过选择合适的距离度量方法,KNN算法能够准确地找出与待分类样本最相似的邻居,从而进行准确的分类。

2. 如何确定K值
在KNN算法中,K值的选择对分类结果具有重要影响。K值太小可能导致过拟合,即算法对训练数据的噪声过于敏感;而K值太大则可能导致欠拟合,即算法忽略了训练数据中的有用信息。
确定K值的常用方法包括交叉验证和网格搜索。交叉验证是一种评估模型性能的方法,它将数据集划分为多个子集,通过多次训练和测试来选择最优的K值。网格搜索则是一种参数调优方法,它通过在一定的参数范围内进行穷举搜索,找到使得模型性能最优的K值。
在实际应用中,可以根据问题的具体需求和数据集的特性来选择合适的K值。通常,可以通过实验和比较不同K值下的分类性能来确定最优的K值。
3. 分类与回归的区别
KNN算法既可以用于分类问题,也可以用于回归问题。
分类问题
给定一个新样本点,KNN算法通常是通过找出训练集中与其最近的k个邻居(根据某种距离度量),然后基于这k个邻居中最常见的类别来预测新样本的类别。
回归问题
如果是回归任务,则是通过计算k个邻居的平均值或其他统计量(如中位数)来预测连续数值。
区别:
分类问题的目标是预测离散型变量,即样本的类别标签;而回归问题的目标是预测连续型变量,即样本的具体数值
4. k邻近算法的步骤
1)距离度量
选择一个合适的距离度量函数(如欧氏距离、曼哈顿距离、马氏距离等),用于计算测试样本与每个训练样本之间的差异程度。
2)确定k值
k是算法中的一个重要参数,表示需要考虑的最近邻居的数量。k值的选择对模型性能有直接影响,较小的k可能导致模型对噪声敏感,较大的k则可能使模型过于保守,倾向于平均结果。
3)搜索k近邻
对于新的测试样本,遍历整个训练数据集,计算它与每个训练样本的距离,并按升序排列,选取距离最近的k个样本作为邻居。
4)决策规则
分类任务:采用多数表决法,统计k个邻居中出现最多的类别,将该类别作为新样本的预测类别。
回归任务:计算k个邻居的目标变量(连续数值)的平均值,将其作为新样本的预测值。
5)边界情况
在分类任务中,如果多个类别的数量相等,则可以设置额外的规则来打破平局(例如使用加权距离、考虑距离远近等)。
四、K近邻算法的优缺点是什么?
优点:
1、KNN算法简单易懂。它的工作原理直观明了,基于实例进行学习,无需建立复杂的模型或进行参数估计。这使得初学者能够轻松理解并应用该算法,同时也便于专业人员快速实现和调试。
2、KNN算法无需参数估计。与传统的参数化模型相比,KNN算法不需要进行复杂的参数训练和优化过程。它直接利用训练数据集中的实例进行分类或回归,从而简化了算法的实现和调试过程。
3、KNN算法适合多分类问题。无论是二分类还是多分类问题,KNN算法都能有效地处理。它通过投票机制确定待分类样本的类别,能够处理具有多个类别的数据集,这使得KNN算法在实际应用中具有广泛的适用性。
缺点:
1、KNN算法的计算量较大,尤其在处理大数据集时。由于KNN算法需要计算待分类样本与训练集中每个样本之间的距离,当数据集规模较大时,计算复杂度会急剧增加,导致算法运行时间较长。因此,在处理大规模数据集时,KNN算法可能不是最佳选择。
2、KNN算法对特征值敏感。算法的性能很大程度上取决于特征值的准确性和完整性。如果特征值存在噪声、缺失或异常值,可能会对KNN算法的分类结果产生负面影响。因此,在应用KNN算法之前,需要对数据进行适当的预处理和特征工程,以提高算法的准确性和稳定性。
3、KNN算法需要选择合适的K值和距离度量方法。K值的选择对算法性能具有重要影响,过小的K值可能导致过拟合,而过大的K值可能导致欠拟合。此外,不同的距离度量方法可能会对分类结果产生不同的影响。因此,在实际应用中,需要通过实验和比较不同K值和距离度量方法下的分类性能,选择最优的参数设置。
4、空间复杂度也较高,因为需要存储所有训练数据。
5、对于大规模数据集和高维数据,效果可能会下降,因为“维度灾难”问题可能导致距离度量失去意义。
6、可解释性差,无法提供决策规则或变量重要性信息。
五、K近邻算法的适用场景是什么?
KNN适用于中小规模、低至中等维度的数据集,在特征空间相对简单或者没有明显规律的情形下效果较好。对于大规模数据集,一般会结合其他技术(如降维、索引优化等)来提高效率。此外,由于其直观性和易于理解性,KNN常被用作教学和快速原型设计的工具。
六、K近邻算法应用场景举例
K近邻算法凭借其灵活性和直观性,在多个领域展现出了强大的适用性和有效性:
- 推荐系统:在个性化推荐场景中,KNN被用于用户偏好预测。例如,根据用户的浏览历史、购买记录等信息,计算新用户与已有用户之间的相似度,然后找出K个最相似的邻居用户。这些邻居用户喜欢的商品或内容将被推荐给新用户,从而实现个性化推荐。另外,KNN还可用于协同过滤技术中,通过分析用户-物品矩阵,找出具有相似行为模式的用户群体,以实现基于邻域的推荐。
- 图像识别:在计算机视觉任务中,KNN常应用于手写数字识别、物体分类等问题。首先,对图像进行预处理并提取特征(如像素直方图、边缘检测特征、纹理特征等),然后利用KNN算法比较待识别图像特征与训练集中各类别图像特征的距离,最终确定图像属于哪一类别。这种方法尤其适用于小型数据集或简单识别任务,而在大规模图像识别任务中,通常会结合深度学习等更复杂的方法。
- 医学诊断与预测:在医疗健康领域,KNN可用于疾病诊断、病情严重程度评估及预后判断等。比如,在肿瘤类型判断上,通过对病理切片的细胞形态学特征、基因表达谱等多种生物标志物进行量化,采用KNN算法对比相似病例,来推测未知样本所属的肿瘤亚型或者预测其恶性程度。此外,对于病人的治疗反应预测,也可以通过比较病史、生理指标等因素相近的病例,利用KNN得出最佳治疗方案。
- 金融市场预测:在金融领域,KNN可以用来预测股票价格走势、评估信用风险等。通过对历史交易数据、财务报表、市场情绪等多个维度的数据进行分析,利用KNN算法寻找与当前市场状况相似的历史时期,并参考当时市场的表现作为未来趋势预测的依据。
- 社交网络分析:在社交网络研究中,KNN有助于发现用户间的隐含关系,实现社区发现或用户兴趣定位。通过衡量用户间的行为相似度(如共同关注的话题、互动频率等),KNN可为每个用户找到社交网络中的“近邻”,进而揭示用户群体的兴趣分布以及社交影响力。
- 物联网(IoT)设备故障诊断:在工业物联网场景下,KNN可用于设备状态监测和故障预警。通过收集设备运行时的各项参数指标,利用KNN对比类似设备的历史故障案例,快速定位当前设备可能出现的问题。
- 电商网站商品推荐:除了上述提到的个性化推荐外,在电商平台中,KNN还可用于关联规则挖掘,根据用户的购物行为和其他用户的行为模式,发现商品之间的关联性,从而推荐相关联的商品。
- 文本分类:文本分类是KNN算法的一个重要应用领域。在文本分类任务中,KNN算法可以将文本数据表示为向量形式,并利用训练数据中的文本向量来分类新的文本数据。例如,在新闻分类中,KNN算法可以根据新闻内容的相 似性将其归类到不同的类别(如政治、经济、体育等)。通过选择合适的特征提取方法和距离度量方式,KNN算法能够有效地处理文本数据中的高维性和稀疏性问题,实现准确的文本分类。
参考:
1、写给产品经理的几种机器学习算法原理-人人都是产品经理-策略产品夏师傅
2、七大机器学习常用算法精讲:K近邻算法(一)-人人都是产品经理-火粒产品
3、【机器学习-13】K-近邻算法(KNN)介绍、应用及文本分类实现
本文由@厚谦 原创发布于人人都是产品经理,未经作者许可,禁止转载。
题图来自Unsplash,基于CC0协议。
该文观点仅代表作者本人,人人都是产品经理平台仅提供信息存储空间服务。
- 目前还没评论,等你发挥!


 起点课堂会员权益
起点课堂会员权益







