编辑导语：有效的用户体验感调研有利于提升产品架构，更好的去完善产品。但是当市场样本量过少，如何科学衡量喜好程度？本文将分享一个数据分析的常见case——威尔逊得分。相信通过本文，可以学到一个更加科学的分析方法，一起来学习下吧。

“分享一个常见的场景，也是经常困扰大家的问题。”

先来一个场景：假设平台售卖两款手机A和B。A手机有800人喜欢，200人不喜欢；B手机有9人喜欢，2人不喜欢。那么，用户更喜欢哪款手机？

相信这个场景，各位朋友在日常生活中、在工作中都遇到过。你们平时是如何做判断呢？希望通过今天的文章，能给大家一个新的视角、也更加科学的方案。

一、常见的衡量方法

我想，大家的第一反应应该是按照比率进行衡量吧？因此，

A手机喜好率=800÷（800+200）=80%

B手机喜好率=9÷（9+2）=82%80%<82%

因此用户更喜欢B手机。

这样对吗？

看起来没毛病。毕竟喜欢率越高，代表用户更喜欢嘛！但是，相信朋友也看出了这个例子的端倪：B手机的总共的样本量才11个，虽然喜欢率高，但是样本量这么低，随便一个数据变化都会对结果产生巨大的影响。

因此，按照这种比率的方法，算出的喜欢率，“靠谱”吗？用统计学的语言，置信吗？

二、威尔逊得分

上面我们觉得按照简单的喜欢率来计算，有点难衡量。但是，如果不按照喜欢率来比较，还能如何计算呢？这就是我们今天的主题了：威尔逊得分。

1. 公式定义

先看看具体的威尔逊得分计算公式：

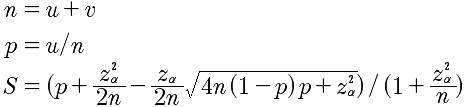
u表示正例数（喜欢），v表示负例数（不喜欢），n表示实例总数（总样本数），p表示喜欢率，z是正态分布的分位数（参数），S表示最终的威尔逊得分。得分越高，代表越喜欢的程度、喜欢的概率越大。

通常，当置信度95%的情况下，z取1.96（近似2）即可。其他常见置信水平与z取值的对应关系如下：

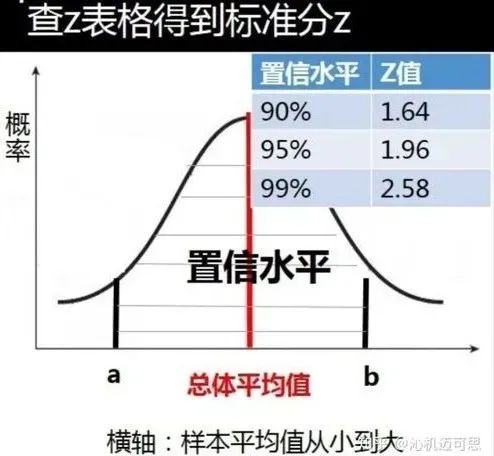
关于置信区间的概念，可以参考文章《区间估计的置信区间概念及方法》。

2. 案例验证

下面，我们根据上面的公式，计算一下我们开头案例的A手机和B手机的威尔逊得分情况。

对于A手机，n=1000，p=0.8，按照95%的置信度，取z≈2，代入威尔逊得分公式中，求得S(A)=0.77

对于B手机，n=11，p=0.82，按照95%的置信度，取z≈2，代入威尔逊得分公式中，求得S(B)=0.52

因此，0.77>0.52，A手机的威尔逊得分高于B手机，按照该算法，我们有结论：在置信度95%的情况下，虽然A手机的喜欢率不如B手机，但是有理由相信用户对A手机其实是更加喜欢的。

3. 相关应用

其实该得分算法的应用还是比较多的。

除了上文中提出的例子外，该得分算法经常应用于各个网站的排序上。比如知乎的搜索排序（我看网上有说知乎是用的威尔逊得分进行的。这里我也没法验证，如果有知乎的朋友可以留言验证一下。关于搜索算法可以参考文章《搜索系统的基础知识以及应用》）：

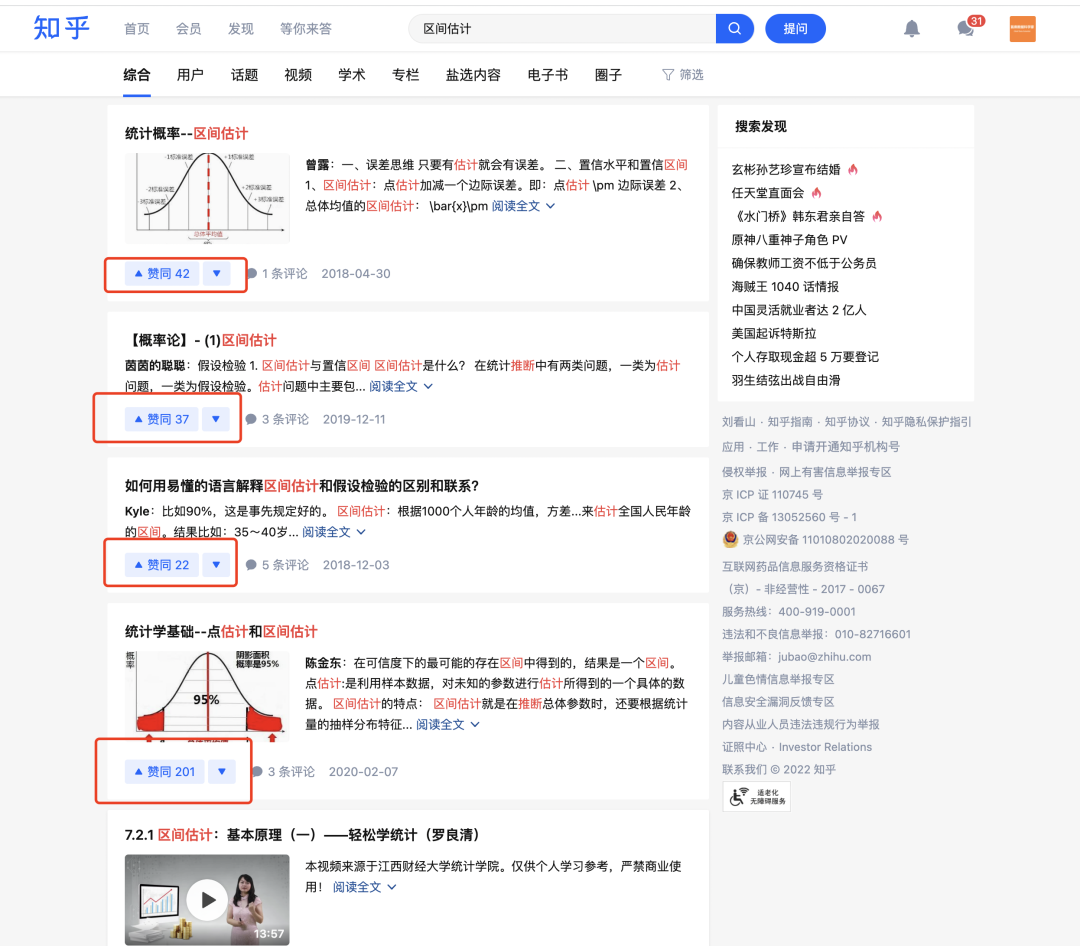
可以看出，知乎的搜索结果排序中，并不是完全基于赞同数量进行的倒叙排列。如果完全赞同数多的回答置顶，那么新的高质量回答，就永远没有出头之日了，对于内容生态的维护一定是有很大问题的。

当然，哪怕是用了威尔逊得分，真实实践中，也会在这个基础上增加更多维度的打分，咱们这里就是以此举例，说明威尔逊得分的应用场景，大家清楚就好。

如果只是想把威尔逊得分作为工具，那么掌握到这里、知道了公式该如何使用、如何计算、应用场景是啥，就足够了。但如果想深入理解一下公式的统计学含义以及推导逻辑，可以参考下面一节。

三、统计原理与逻辑

下面，我们一起看看这个威尔逊公式是怎么得到的，以及背后的统计学原理是啥。

1. 原理概述

首先，威尔逊得分只是威尔逊区间的一个变形，取了威尔逊区间的下限值作为威尔逊得分。

那什么是威尔逊区间呢？

本质上，威尔逊区间其实就是用户喜欢率的一个区间估计（关于区间估计可参考历史文章《区间估计的基础介绍》）。但是该区间估计考虑了样本过小时候的情况，根据样本量对区间估计进行了修正，使得该区间估计能够较好的衡量不同样本量情况。

说白了，我们用样本计算的用户喜欢率，本质上只是对用户真正的喜欢率的一个点估计而已，样本越少，可信度越低；样本数越多，根据中心极限定理，点估计越接近真实值。如果样本数都很多，那么我们直接计算手机A和B的喜欢率，基本就能代表真实情况了，是可以比较的。但是当样本数不够，就面临了上文中的问题。威尔逊，就是1920年代提出了这个区间估计的公式，用以解决小样本的准确性问题。

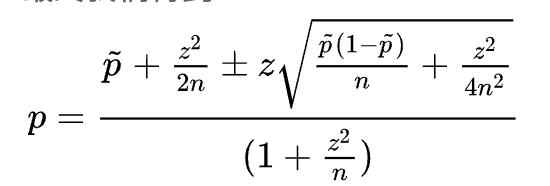
由于提出的公式是区间估计公式，所以本来是一个一个的区间。比如假设A手机的喜欢率95%置信区间估计是[0.77,0.83]，B手机喜欢率95%的置信区间估计是[0.52,1]。如何对比两个区间呢？威尔逊得分就是取了不同区间的下限进行比较，因此哪个下限高，代表概率更高。

2. 公式推导

这里的公式推导其实还是有点复杂的，我不一一展开了，放一下网上的推导步骤截图，有兴趣的朋友可以自行探索一下啊！

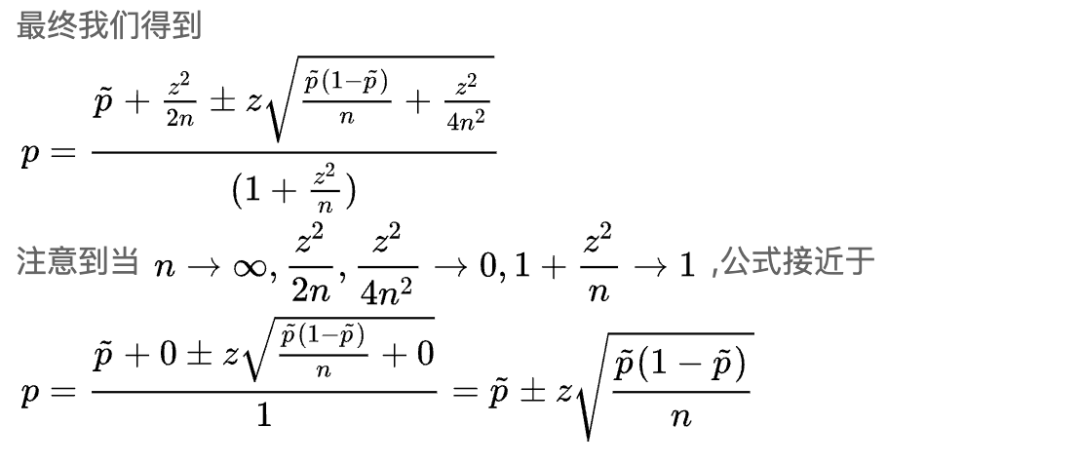
3. 性质特性

最后我们看看这个公式的一些性质吧。

• 性质1：得分S的范围是[0,1)，效果：已经归一化，适合排序
• 性质2：当正例数u为0时，p为0，得分S为0；效果：没有好评，分数最低；
• 性质3：当负例数v为0时，p为1，退化为1/(1 + z^2 / n)，得分S永远小于1；效果：分数具有永久可比性；
• 性质4：当p不变时，n越大，分子减少速度小于分母减少速度，得分S越多，反之亦然；效果：好评率p相同，实例总数n越多，得分S越多；
• 性质5：当n趋于无穷大时，退化为p，得分S由p决定；效果：当评论总数n越多时，好评率p带给得分S的提升越明显；
• 性质6：当分位数z越大时，总数n越重要，好评率p越不重要，反之亦然；效果：z越大，评论总数n越重要，区分度低；z越小，好评率p越重要；

4. 变形扩展

另外，我们这里都是二项分布。如果是评分等级问题：如五星评价体系，或者百分评价体系，该怎么办呢？

将威尔逊得分的公式由伯努利分布修改为正态分布，带入相关参数即可。

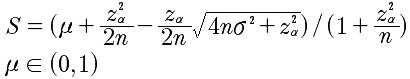
注意：均值和方差均是归一化之后的数值。

关于威尔逊得分，我们就分享这些，希望对大家今后的数据工作能有所帮助。以后再衡量哪个更好，可以有更专业的算法模型了！

#专栏作家#

NK冬至，公众号：首席数据科学家，人人都是产品经理专栏作家。在金融领域、电商领域有丰富数据及产品经验。擅长数据分析、数据产品等相关内容。

本文原创发布于人人都是产品经理。未经许可，禁止转载。

题图来自Unsplash，基于CC0协议。