A/B测试在产品优化中的应用方法是：在产品正式迭代发版之前，为同一个目标制定两个（或以上）方案，将用户流量对应分成几组，在保证每组用户特征相同的前提下，让用户分别看到不同的方案设计，根据几组用户的真实数据反馈，科学的帮助产品进行决策。

是什么

生物学以及其他学科中，总是会出现「控制变量法」来验证某种假设。通常有一组对照组、一组试验组，比如：

证明：酶在加热到一定温度后会失活。

第一次向反应体系中加入加热后的酶；第二次加入没加热的，看反应现象。其中，第一次为实验组，第二次为对照组。

证明：吸烟会增大得肺癌的几率。

我们可以选两群位于同一地区、职业类似人，一群人吸烟，一群人不吸烟，进行跟踪调查，样本容量要足够大。其中吸烟的那组为实验组，不吸烟的为对照组。

以上算是A/B实验的引子和简单案例。到了真正的科研领域中，会有更严谨的应用方法。而A/B测试被应用到产品设计上，最早可查的是在2000年开始，Google的工程师才开始使用A/B测试进行产品设计。

在产品设计中如何应用，直接引用一段：

A/B测试在产品优化中的应用方法是：在产品正式迭代发版之前，为同一个目标制定两个（或以上）方案，将用户流量对应分成几组，在保证每组用户特征相同的前提下，让用户分别看到不同的方案设计，根据几组用户的真实数据反馈，科学的帮助产品进行决策。

「将用户随机均质分组后，应用不同的方案，观察各组的数据反馈，以指标的高低衡量方案的好坏。」

听起来没什么问题，对吗？

说实话，对于A/B测试是什么，大部分人对它的理解就停留在这个层面上，误以为这就是A/B测试的全部了。这就跟梅超风仅偷了《九阴真经》的下册一样，真本是真本，就是不知道怎么打基础结果路子全歪了。

我们可以用Excel来模拟试试，用随机生成1000个样本，再随机分成对照组和试验组2组，然后去比较这2组的平均值——你会发现2组之间一定会有差异，不信你可以亲自试试。

但这能说明其中一组比另一组要好吗？当然不能。如果你把用户分成两组，用不同的方案监测转化率差别，并且试验组正巧比对照组效果好一点，那你如何能证明，试验组更好不是因为这种随机波动产生的呢？

我曾经不只一次听到过类似「指标一会儿高一会儿低，测不出来效果」或者「跑了很久汇总比较，指标变高了效果不错」这样的说法，甚至还是出自专业人士之口，实在让人目瞪口呆，感叹原来A/B居然还能这么做。

法 → 为什么

我们什么都没干、什么方案都没有实施，只是随机分了一下组，试验组就比对照组更好或者更坏了。所以很显然我们不能直接以结果指标的高低衡量方案的好坏。因为无论怎么随机分组，都会因为分组产生一定的选择偏差，导致数据出现波动，那我们应该如何验证不同方案的好坏呢？

这时候，就轮到统计学的「假设检验」出场了，这才是《九阴真经》的上册，是练就绝世武功的基础。

我们从最简单的抛硬币的实验说起。不过这次不是一个硬币，是有两枚硬币。

有人宣称他有特殊的抛硬币技巧，应用了他的技巧，可以让硬币更容易出现正面。那我们要如何才能证明他说的是真的呢？人家又没有说次次都是正面，就算10次抛出来都是反面也可以说是状态不好发挥失常。

怎么办？我们可以用逆向思维反过来想，如果他说的是真的，那么用他的技巧抛硬币就不太可能经常抛出反面，更不可能抛100次都是反面。也就是说，不可能发生的事件发生了，那他就在说假话。

用统计学语言来描述，就是：对于一个假设，在这个假设成立时，一个极小概率的事件发生了，就可以推翻这个这假设，并选择这个假设的反面。一般把待证伪的假设称为「零假设H₀」 ，把想要证明的假设叫做「对立假设H₁」。

这就是「反证法」，一条假设永远不可能被证明，只可能被证伪。

我们想证明「他的技巧抛硬币更容易出现正面（对立假设）」，可以先假设「他的技巧不能让抛硬币更容易出现正面（零假设）」，然后寻找在零假设成立时的极小概率事件（比如用他的技巧抛100次硬币比正常抛硬币，正面出现的频次高30%），当这个极小概率事件被我们观测到的时候，就推翻了零假设，从而证明对立假设。

这里对于多小的概率是「极小概率」，完全是人为规定的，一般常用的是5%和1%。这个值就是所谓的「显著性水平」ɑ。假定我们抛10次，我们这一批10次观测到的结果发生的概率就是p值，比如

抛10次结果都是正面，这种情况发生的概率是：

当我们观测到这样一个 p ≤ ɑ 时，就可以推翻零假设，从而证明「他的技巧抛硬币更容易出现正面（对立假设）」。

现在，重点来了：我们可以把「新的产品设计方案」当作「他的特殊技巧」，把「每有一个用户」当作「每一次抛硬币」，把「用户被转化」当作「硬币为正面」，把「用户未被转化」当作「硬币为反面」，瞬间就会理解如何在产品设计中进行科学的A/B测试。

不同的是，我们已经根据日常经验建立了对抛硬币「转化率」和「波动水平」的大致预期。简单来讲，就是如果特殊技巧抛硬币的「转化率」只是51%、52%的水平，我们显然会怀疑特殊技巧的有效性，而如果能到60%，我们几乎可以认定特殊技巧确实有效。

而对于产品「转化率」和「波动水平」很难建立同样的预期。「转化率」从10%到12%，究竟是日常波动，还是巨大提升，在不进行统计分析时是根本无法判断的。

术 → 怎么做

统计理论展开讲就太复杂了，所以我只介绍如何应用现成的理论和公式。

我们在产品设计时设计的A/B测试属于「双独立样本t假设检验」，「独立」的意思是A方案下样本和B方案下的样本表现是各自独立互不影响的。比如抛硬币案例里普通人抛硬币和他用特殊技巧抛硬币，结果互不影响。t没有什么特殊含义，如果是周树人用笔名发表了这套检验理论，那t检验就会被叫做鲁迅检验了。

按照「双独立样本t假设检验」的方法，需要计算以下几个统计量：

（1）每组样本均值x

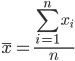
（2）每组样本方差S

（3）计算自由度（基于双样本异方差假设）

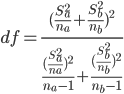
（4）查表取得ɑ/2（双尾检验）下的t-value，我们当然不会真去查表，直接使用Excel函数=T.INV.2T(ɑ/2,df)

然后就可以套公式计算置信区间了：

之所以用双尾检验的t-value，是因为习惯做的零假设是「A和B之间没有变化」，对立假设是「A和B之间有变化」，通过实验判断是否能推翻零假设，再根据结果的正负判断是变高还是变低。
看完上面的公式是不是感觉好复杂？没关系，有简单的方法。

如果只想知道p-value以验证实验结果是否统计显著，而不需要计算置信区间，可以用Excel函数

=T.TEXT(array1, array2, 2, 3)

如果一定要计算置信区间，可以用RStudio：

t.test(array1, array2, conf.level = 0.95)

一步出结果，够方便了吧。

应用的前提条件：

应用上述公式，是有前提条件的。简单来讲就是样本独立，且要服从正态分布，并且两总体方差不等（异方差）。如果样本不独立，比如同一批病人用药前和用药后的效果检验，就要使用配对t检验。如果样本独立但总体方差相等，就要用另外的一套公式。

那岂不是应用之前还要做很多分析判断该用哪个公式？

其实不然。根据统计学的中心极限定理，在大样本下，样本均值的抽样分布呈正态分布。而我们做的A/B测试，几乎都是独立的十几万、几十万的样本，并且可以假定A/B总体异方差。

一点提示：

关于假设检验的计算，能很容易地找到很多资料。不过质量参差不齐，可以用一个粗暴的办法识别质量过得去的：

1. 统计学中的一般表示方法，样本均值是x-bar，总体均值是μ，样本标准差是S，总体标准差是σ，样本个数是n，总体个数是N，用反了虽然不能算错但就不专业了；
2. 求样本方差时分母是自由度n-1而不是样本个数n，一般我们做的A/B试验都是大样本，用哪个当分母没什么区别，但如果真碰到小样本（不足30个）的实验，区别就很大了；
   能保证以上两点都很严谨的资料，基本都是有统计学背景、可以确定质量过得去了。

   道 → 凭什么

   为什么要进行A/B试验？如果最后都要A/B试验来做决策，那还要产品经理做什么？

一定会有老板喜欢这样发问。对于这样的老板，我们可以把俞军大神请出来猛烈地拍回去。

受俞军产品方法论的启发，我的理解是：

每一款产品，都有独特的、与其他产品不完全相同的用户群体，每一次A/B测试，都是对于当下用户更进一步的理解，是对「用户模型」的又一次完善。

一次与预期结果相悖的A/B实验，也是成功的实验，因为它让我们能更加了解目标用户的偏好，了解他们喜欢什么、不喜欢什么。说白了，A/B测试是让我们深刻理解用户的科学工具，而不单单只是衡量产品方案好坏的天平。

而这一点，是用户访谈所回答不了的，也不是产品经理和设计师们靠个体的经验和认知能回答的。因为「用户不是自然人，是需求的集合」。只有在统计结果下，我们才能认清「用户群体」的真面目。对于C端用户，应该用统计的思维去理解。不要「你觉得」，也不要「我觉得」。

参考资料：

1. 概率论与数理统计，陈希孺
2. 面向数据科学家的实用统计学，[美] 彼得·布鲁斯 / 安德鲁·布鲁斯
3. 俞军产品方法论，俞军
4. 数据驱动设计：A/B测试提升用户体验， [美]罗谢尔·肯
5. https://zh.wikipedia.org/wiki/%E5%AD%B8%E7%94%9Ft%E6%AA%A2%E9%A9%97，学生t检验

本文由 @Guibin 原创发布于人人都是产品经理。未经许可，禁止转载

题图来自Unsplash，基于CC0协议