生活中无处不在的贝叶斯理论,对我们到底有什么启发?
文章从三扇门问题切入,解读贝叶斯理论的核心逻辑,并用生活案例说明其应用。同时分享该理论对普通人的启发,助力在不确定性中理性决策。

选山羊还是汽车
去年有幸参加了杜继南老师《落子无悔·科学决策》的线下课程,课上杜老师提出了经典的贝叶斯三扇门问题。好巧不巧,最近读《思考快与慢》,丹尼尔.卡尼曼多次提到贝叶斯理论,正在这时有幸收到中信出版社《贝叶斯定理》纸质图书,这些巧合都在推动我快写一写贝叶斯理论吧。毕竟贝叶斯公式可是被号称为“上帝公式”,在生活中无处不在。
那今天就从有意思的三扇门问题开始吧。
了解贝叶斯理论的人,应该知道这个问题,大致是这样的:
你去参加一个节目,主持人告诉你:
现在有三扇门,门后分别藏有一只羊或一辆轿车,总共有2只羊、一辆轿车。
你可以选择其中一扇门背后的东西带回家(因轿车比山羊贵,我们默认大家都想选出轿车带回家)
在没有任何其他信息的情况下,你随机选择了1号门。
这个时候主持人说,为了提升选中轿车的概率,他现在可以打开剩下2扇门中一扇,于是他打开了3号门,是山羊。现在主持人问你要不要换2号门?
那我们到底该不该换呢?(大家可以现根据直觉判断要不要换,了解完贝叶斯理论后,再回过头来看咱们的决策是否科学)
这就是一个很典型的贝叶斯问题?那到底什么贝叶斯定理,他又能怎么帮助我们决策呢?
01 到底什么是贝叶斯理论
叶斯理论是一个后验概率,它根据已知信息算出事件发生的概率。比如前面三扇门问题“主持人打开了3号门,是一只羊”,这个就是已知信息,它的计算公式是:
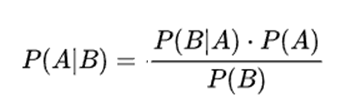
上学时觉得这个公式很简单,直到再次读到贝叶斯时,发现很容易搞错。很多人觉得看到公式就头疼,那是因为没有理解他,接下来我们一起来拆解:
A、B分别为两个事件,P表示概率,|表示条件,P(A|B)即表示在事件B发生的条件下,事件A发生的概率。
从上面的公式可以看出,要想知道“在事件B发生的条件下,事件A发生的概率”,我们必须知道三个数据:
① P(A):这个我们叫做先验概率,即没有条件限制的情况,事件A一般发生的概率。
② P(B | A):似然概率,事件A发生的条件下事件B发生的概率。
③ P(B):边缘概率,即事件B发生的概率。
举个例子来说明:
比如几年前新冠流行时,事件A为感染新冠,事件B为试纸测出阳性,现在我们想知道测出阳性的条件下实际感染新冠的概率P(A|B)。
假设:
P(A)=20%(即某地区新冠的整体感染率20%)
P(B | A)=90%(试纸测试的准确度90%,即健康人假阳性的概率为10%,患者假阴性的概率为10%),现在某人试纸测出了阳性,请问此人实际感染新冠的概率是多少?
很多人会说,当然是90%了,事实并不是,我们一起按照公式计算。
P(A|B)= P(A)* P(B | A)/ P(B),根据上面的信息我们需要计算出P(B),即试纸为阳性的概率(包括健康人群、患者人群)
P(B)= P(B健康)+ P(B患者)=80%10%+20%90%(80%的健康人群阳性的概率是10%,20%患者人群阳性的概率为90%)=80%
P(A|B)= P(A)* P(B | A)/ P(B)=20%*90%/80%=22.5%
很多人会说,可是我们实际测试时一般认为测出阳性,就感染了呀,这里的计算为什么只有20%多点的概率?跟实际不符合。
这是因为实际我们仅针对高危人群测试,比如有症状的,或者密接,这种时候P(A)也许达到90%。我们计算概率,一定要看对应的条件,不同条件下概率差别很大。
比如某地区一天下雨的概率只有5%,但在乌云密布的条件下,下午的概率就高达90%。
汤姆·奇弗斯在《贝叶斯定理》一书中还举了一个颠覆认知的例子,叫“检察官谬误”。
我们都知道DNA检测是锁定嫌疑人的重要手段,那我们能否因为DNA匹配这一项线索去锁定嫌疑人呢?
假定你正在做犯罪调查,在凶器上采集到了DNA样本,且该样本与该国家6800万人样本库中某人的DNA匹配(DNA的匹配度非常高,平均每300万人中才能有1人匹配),这是否意味着此人是凶手的概率为99.99997%(1-1/300万)呢?
并不是!
按照1/300万的匹配度,那么6800万人样本中就有6800万*1/300万=20人的DNA是匹配的,但是凶手只有一个,意味着在没有其他信息输入的情况下,此人是凶手的概率仅为1/20=5%。
没想到吧,要想抓到凶手仅凭DNA这一项是不够的,得通过其他线索不断缩小范围。
讲了这么多,想必大家对贝叶斯定理已经有了初步理解。但或许有人会觉得,这玩意太过学术,感觉日常也用不上。
并不是!
贝叶斯被称之为“上帝公式”,生活中随处可见。接下来,我们就聊聊,贝叶斯理论对于我们普通人有什么启发。
02 经验直觉解决大部分问题,小心认知陷阱
是的,我们生活大部分问题不需要经过复杂的思考,按照直觉走一般不会出太大差错,我们的直觉通常来自过往经验,即贝叶斯公式的先验概率。
但很多时候,这种直接会给我们带来认知缺陷。比如,扩大罕见事件的影响。比如,当我们听到飞机坠毁事故后,身边很多人不愿意再选择坐飞机,而改用坐汽车等替代。但实际上,坐飞机比汽车更安全。据WTO数据统计,飞机的死亡率约0.05/十亿公里,汽车的死亡率约3.1/十亿公里,汽车的风险是飞机的60倍!单从安全角度,选择坐汽车替代飞机,这就是认知陷阱。
03 动态提升,在不确定性中获利
整个世界是充满不确定性的,我们不能完全依赖于过往的经验,去对未来做出判断。
比如小王上班,过往经验下迟到的概率5%,我们可以说小王今天大概率不会迟到吗?如果当天暴雨,小王乘坐的地铁出现了故障,这个时候我们还能说小王大概率不会迟到吗?
贝叶斯公式是一个后验概率,他会根据获得的新信息不断更新算法,现在的AI、机器学习、大模型应用,都是运用了贝叶斯理论。
4 量化概率,科学决策
我们讲话很多时候喜欢用“可能”,比如我说“A股票明天可能会涨”,第二天这个股票确实大涨了,我会觉得自己特别厉害,预测精准。但如果跌了呢,我也不觉得自己有问题,因为我说的是“可能”嘛,可能涨就有可能跌,于是“A股票明天可能会涨”其实是一句废话。
但是加上概率就不一样了,“A股票明天90%会涨”这句话是有明显的倾向了,如果我是炒股大佬,释放的就是乐观信号。
当然我只是举例子,事实上股价这种东西参照丹尼·卡尼曼的说法“根本无法预测”。
再回到我们开头的例子,如果没有量化的概率,我换门、不换门都很难说出理由,靠直觉。如果我们计算出不换门、换门选中汽车的概率,一对比就很清楚到底要不要换门了。
2只羊、1辆汽车分别放在三扇门后,我们没有任何其他信息,因此每扇门后是汽车的概率均为1/3(这是一个先验概率)。
现在主持人打开了3号门(是羊),假定一开始我们选中了1号门,现在要不要换成2号门呢?需要我们来看看1、2号门背后是汽车的概率分别是多少?
事件①:1号门后是汽车;事件②:2号门后是汽车;事件③:3号门后是羊(主持人只可能打开背后是羊的门),已知p(①)=p(②)=1/3,p(③)=2/3,求p(①|③)、p(②|③)。
通过计算可知:
p(①|③)= p(③|①)* p(①)/ p(③)=(50%*1/3)/(2/3)=25%
p(②|③)= p(③|②)* p(①)/ p(③)=(100%*1/3)/(2/3)=50%
可以看出,在已知3号门是羊的情况下,汽车在1号门、2号门后的概率分别为1/4,1/2,因此我们要换门(这个答案跟你刚开始的直觉一样吗)。
为了便于理解,说明下p(③|①)、p(③|②)的数据怎么来的:
p(③|①):即汽车在1号门,主持人打开3号门的概率,因为主持人肯定会选择打开是羊的门,当1号门是汽车时,主持人会随机在2、3号门中打开一扇门,因此打开3号门的概率50%。
p(③|②):即汽车在2号门,主持人打开3号门的概率,这个时候主持人不可能打开1、2号门,因此打开3号门的概率为100%。
写在最后
贝叶斯公式是一种思想,并不需要我们去计算复杂公式,而是在通过经验判断的同时,保持理性,去思考决策背后的概率大小,并根据获得新信息不断更新迭代。
关于贝叶斯本人及贝叶斯思想的应用,推荐阅读汤姆·奇弗斯在《贝叶斯定理》。
本文由人人都是产品经理作者【运营小羊】,微信公众号:【运营小羊】,原创/授权 发布于人人都是产品经理,未经许可,禁止转载。
题图来自Unsplash,基于 CC0 协议。
- 目前还没评论,等你发挥!


 起点课堂会员权益
起点课堂会员权益







